Lisää talja-analyysia

Kehittelin aiemmin talja-analyysia muutaman tekstin verran. Sieltä jäi kutittelemaan pari irtonaista johtolankaa, joten otetaan asiaa hieman penkille.

Yritänpä pyöräyttää määritelmän: Talja on järjestely, jossa joukko köysimäisiä elementtejä sitoo toisiinsa ankkurin, taakan ja vetävän elementin, kuten käden. Sanotaan kaikkia näitä yleisesti elementeksi. Köysimäiset elementit liittyvät muihin elementteihin joko suoraan (kuten solmulla tai tarraimella) tai kulkemalla köysipyörän kautta, joka taas on osa toista elementtiä. Kaikki elementit ovat sikäli samalla suoralla, että köysimäisten elementtien voi katsoa olevan yhdensuuntaisia ja siis köysipyörän kautta kulkevat tekevät pyörässä 180º käännöksen. Talja on staattisesti määrätty järjestelmä, jos ja kun oletetaan että kaikki köysimäiset elementit pysyvät vedossa, joten jokaisen elementin asento riippuu yksiselitteisesti alkutilanteesta ja vetävän elementin asemasta.

Määritelmään ei kuulunut se, että taljaa voidaan käyttää voiman kasvattamiseen, koska myös voimaa pienentävä tai lukuisista pyöristä ja elementeistä huolimatta voiman samana säilyttävä talja on edelleen talja. Myöskin resetoitavuus jää tuon määritelmän ulkopuolelle, ja tietyllä tavalla se onkin taljan tässä käsiteltävään funktioon liittymätöntä asiaa.

Keskitytään erityisesti sellaisiin taljoihin, joiden ideaalin voimakertoimen saa ratkaistua yksinkertaisella voima-analyysilla, jota joskus myös T-menetelmäksi kutsutaan. Tämä edellyttää aiemman määritelmän lisäksi, että jos voima haarautuu taljan jossain kohdassa, se tapahtuu tietyllä tavalla. Täsmennän tätä kunhan on hieman sukelleltu.

Vielä pari määritelmää evääksi: Ideaali(se)lla tarkoitetaan tässä kitkatonta. Laskennallisella tarkoitetaan sellaista, jossa kitkan vaikutus yritetään huomioida. Hyötysuhde on välillä 0 ... 1 oleva luku, joka kertoo kuinka iso osa energiasta on kitkahäviöiden jälkeen jäljellä. Voimakerroin on se luku, jolla talja kertoo voiman (ja etenkin jolla saavutettava matka vastaavasti jaetaan). Efektiivinen voimakerroin on todellinen, siis toivottavasti sama kuin laskennallinen.

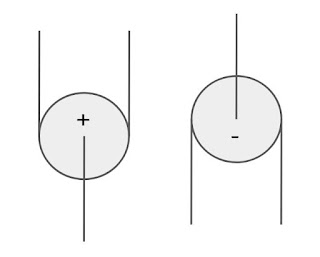
Esimerkiksi Z-rigissä (yksinkertainen 2 pyörän suuntaavaihtamaton talja) on kolme köysielementtiä (E1, E2 ja E3), ankkuri (G), kuorma (L) ja vetävä elementti (F). Kun taakka nousee, liikkuvat elementit E1 ja E3 ylöspäin ja elementti E2 alaspäin. Määritellään "ylöspäin" positiiviseksi suunnaksi ja ylöspäin liikkuvaa elementtiä positiiviseksi elementiksi. Vetävä elementti on esimerkin tapauksessa positiivinen, kuten taakan elementti L, mutta osa taljoista on suuntaa vaihtavia, jolloin vetävä elementti ja taakka ovat erimerkkiset.

Köysipyörän idea on vaihtaa köyden suuntaa vähentämättä köydessä olevaa voimaa. Ideaali köysipyörä voi siis kaksinkertaistaa voiman kaksinkertaistamalla köyden, vaikka tätä köyttä edelleen kiristettäisiin vain toisesta päästä. Oikeassa maailmassa köysipyörän (tai tarkemmin pyörän ja köyden yhdistelmän) hyötysuhde on selvästi alle yksi, joten voima ei aivan kaksinkertaistu.

Jos vetävällä puolella on voima F, pyörän toiselle puolelle saadaan voima P*F, jossa P on pyörän P hyötysuhde (esim 90% = 0,9). Siispä pyörän toiselle puolelle tuleva voima on F + P*F eli F + PF. P:n arvolla 0,9 summa olisi siis 1,9F eli 1,9-kertainen voima vetävään voimaan nähden. Kutsutaan tätä laskennalliseksi voimakertoimeksi.

Tämä talja oli yksinkertaisin mahdollinen voimaa lisäävä talja, yksinkertainen 2:1 eli V-rig. Monimutkaisemmatkin taljat voidaan analysoida samalla tavalla ja laskea niille (laskennallinen) voimakerroin. Koska köysipyöriä on kaikissa muissa voimaa lisäävissä taljoissa enemmän, ne täytyy toki numeroida P1, P2 jne. Esimerkiksi mainio 5:1 jota olen kutsunut crevasseksi ja sitten hukannut lähteen tälle nimelle:

Tässä siis ei suotta ole kuljetettu voiman suuruutta F mukana, vaan luvut ovat F:n kertoimia alkaen vetävästä voimasta 1. Nähdään muutamia mielenkiintoisia asioita. Ensinnäkin termien määrä on sama kuin taljan ideaali hyötysuhde 5. Kun jokainen termi saa hyötysuhteista riippuen arvot 0 < P < 1, on summa eli laskennallinen voimakerroin välillä 1 ... 5, eikä millään ilveellä voitaisi saada parempaa arvoa kuin viisi.

Toiseksi, riippumatta pyörien hyötysuhteesta saadaan tosiaan aina vähintään vetävä voima sellaisenaan, ensimmäinen termi "1". Tämä johtuu siitä, että vaikka kaikki pyörät olisivat totaalisen jumissa ja köydet niihin tahmaantuneita niin että köyden voisi yhtä hyvin solmia pyörään kiinni (P1=P2=P3=0), kuormalle välittyy silti voima 1 (*F). Suuntaa vaihtaville taljoille tämä ei tietenkään päde.

Edelleen jatkamalla ajatusleikkiä köysipyörien jumittamisesta voidaan ymmärtää jonkinlaiset perustelut kullekin termille. Esimerkiksi P2 vastaa sellaista voiman tai energian reittiä taljassa, jossa pyörät P1 ja P3 on kokonaan jumitettu. Tähän tapaan:

Punainen reitti on siis sellainen, jossa energia ei kulje yhdenkään pyörän läpi, joten yksikään hyötysuhde ei pääse sitä nakertamaan. Sininen reitti on vain pyörän P2 läpi, joten sitä pitkin kulkevaa energiaa verotetaan P2:n mukaan. P1P2 kulkee tietenkin pyörien P1 ja P2 kautta ja niin edelleen.

Miksi ei ole olemassa termiä P1? Koska ei ole mitään reittiä, jota energia voisi kulkea P1:n kautta niin ettei se kulkisi myös P2:n kautta. Kuinka se edes voisi olla mahdollista, koska P1 kääntää kuormalta tulevan voiman alaspäin, ja tässä taljassa veto on ylöspäin. Tapahtui P1:n ja vetävän elementin välillä mitä vain, suunta ei missään tapauksessa vaihdu ilman toista pyörää, tässä tapauksessa P2.

Tästä päästään huomioon: Jos taljassa on vastakkaisiin suuntiin vetäviä köysipyöriä, niistä osa vääjäämättä jää ilman omaa termiään. Kutsutaan tämän esimerkin pyörien P2 ja P3 suuntaa positiiviseksi ja P1 negatiiviseksi:

Vaikken sitä tähän hätään edes yritä formaalisti todistaa, miinusmerkkisellä pyörällä ei koskaan ole omaa termiään, paitsi jos talja on suuntaa vaihtava - ja yleisemmin sellaisella köysipyörällä ei koskaan ole omaa termiään, jonka merkki on eri kuin vetävän elementin. Mitä merkitystä tällä on? Ensinnäkin pienten kertalukujen termit 1, ja P ovat kokonaishyötysuhteen kannalta oleellisimpia. 1 on nollannen asteen termi ja arvoltaan aina sama, mutta ensimmäisen asteen termi kuten P2 riippuu köysipyörän hyötysuhteesta. Oletetaan että se on 0,8. Jos myös P1 on 0,8, on termin P1P2 arvo 0,64 - koska tällä reitillä molemmat pyörät verottavat energiaa. Silti tämä termi on ikään kuin tasavertaisena yhtenä viidestä ponnistelemassa kohti ideaalia voimasuhdetta 5:1.

Vedetään ehkä hieman hätäinen johtopäätös: olisi edullista, jos taljan laskennallisen voimakertoimen termit olisivat ainoastaan nollatta ja ensimmäistä astetta. Nollannen asteen termejä "1" on aina vain yksi, koska kulkematta köysipyörän kautta ei voimaa saada taljassa kasvatettua. Mutta mitä rajoituksia on ensimmäisen asteen termien määrällä? Voisiko rakentaa kolmesta 80% köysipyörästä taljan, jonka ideaali voimasuhde on 4:1 ja laskennallinen voimasuhde on 1+P1+P2+P3 = 3,4:1?

Ja toisaalta mitä rajoituksia on termien määrällä ylipäätään, koska se näyttää määräävän taljan ideaalin voimasuhteen?

Tutkitaanpa ensin paria muuta esimerkkitaljaa vastaavasti analysoituna.

Laskennallinen voimakerroin ) 9:1:lle on
1 + P2 + P4 + P1P2 + P2P4 + P3P4 + P1P2P4 + P2P3P4 + P1P2P3P4

ja 11:1:lle
1 + P2 + P4 + P1P2 + P1P4 + P2P4 + P3P4 + P1P2P4 + P1P3P4 + P2P3P4 + P1P2P3P4

Koska taljat ovat suuntaa vaihtamattomia eli ylöspäin vedettäviä, molemmissa on taas nollannen asteen termi. Molemmissa on myös neljännen asteen termi P1P2P3P4, joka vastaa sitä energian reittiä joka kulkee kaikkien pyörien läpi. Aivan kuten nollannen asteen termejä, myöskään tätä korkeinta astetta (sama kuin pyörien määrä) ei oletettavasti voi olla yhtä enempää, tosin tätä en taida osata osoittaa.

Jonkinlaisena aihetodisteena kuitenkin huomautan, että kunkin energian reitin (esimerkiksi P1P2P3) pitäisi esiintyä korkeintaan kerran, koska tällä reitillä kerta kaikkiaan on vain yksi köysi. Samoin kukin pyörä esiintyy korkeintaan kerran kussakin termissä, koska yhdenkään pyörän läpi ei mene kahta (kierrosta) köyttä. Ehkäpä vielä tavoitan hieman formaalimman tason tässä todistelussa.

Mutta jos nyt oletetaan että

• Yksi pyörä esiintyy korkeintaan kerran yhdessä termissä ja
• Kahta samanlaista termiä ei koskaan esiinny,

seuraa kiinnostavia asioita. Merkitään nämä ehdot täyttävät termit asteluvuittain nollan, yhden, kahden, kolmen ja neljän köysipyörän taljoille (nollan pyörän talja muuten on vain suora köysi):

Tässä saattaa olla matematiikasta kiinnostuneille jotain tuttua. Ensimmäisellä rivillä 1, toisella rivillä 1, 1, kolmannella 1,2,1, neljännellä 1, 3, 3, 1 ja viidennellä 1, 4, 6, 4, 1. Kyseessä on Pascalin kolmio. Luetellut luvut ovat kombinaatioiden määriä, ja kombinaatiot ovat erilaisia tapoja poimia osajoukko. Esimerkiksi alimmalla rivillä liila kuuden joukko on ne parit, kahden alkion kombinaatiot, jotka voidaan poimia joukosta P1, P2, P3 ja P4.

Pascalin kolmiosta tiedetään esimerkiksi, että rivien alkioiden summa on 2^N (2 potenssiin N), jossa N on rivin järjestysluku, kun ylintä riviä sanotaan nollanneksi.

Toisin sanoen aiemmin asetetuilla ehdoilla N:stä köysipyörästä rakennetun taljan voimakertoimen lausekkeessa voi olla maksimissaan 2^N termiä. Ja koska kunkin termin arvo ideaalitapauksessa on 1, on taljan ideaali voimakerroin maksimissaan 2^N. Esimerkiksi nollalla pyörällä saa voimakertoimen 2^0 = 1 (pitää paikkansa jopa oikeassa maailmassa), yhdellä 2^1=2 (V-rig) ja kolmella 2^3=8.

Onko sellaisia taljoja oikeasti olemassa, joilla saisi aikaan näitä pyörien määrän puolesta maksimaalisia kertoimia? Kyllä on, ja teräväpäinen saattaa heti keksiä kahden potensseista, mistä on kysymys. Myös aiemmin vastaan tullut päätelmä, ettei suunnaltaan negatiivisella pyörällä voi olla ensimmäisen asteen termiä, antaa hyvän vinkin. Kaikkien pyörien on siis oltava positiivisessa suunnassa, ja jokaisen pyörän olisi kaksinkertaistettava voima.

Kyllä, "V on V on V jne." on juuri sellainen. Esimerkiksi kuvan kolmen pyörän taljan lausekkeeksi saadaan (pyörien numeroimisesta riippumatta)

1 + P1 + P2 + P3 + P1P2 + P1P3 + P2P3 + P1P2P3.

Bingo, jokaisessa ruudussa rasti ja siis ideaali kerroin 8:1. Tämähän ei tee kyseisestä taljasta ollenkaan erityistä. V on V eli "piggyback" on ihan käyttökelpoinen (ja oletettavasti ainut tapa saada kahdella pyörällä aikaan 4:1-talja). Mutta ainakaan tämä 8:1 ei ole kovin käytännöllinen kaikkine resetointitarpeineen päivineen. Myöskään talja ei välttämättä ole mikään hyötysuhteen eli efektiivisen voimakertoimen riemuvoitto: nythän on maksimoitu paitsi terveellisten ensimmäisen asteen termien määrä, myös toisen ja kolmannen asteen termien määrät.

Termeille tosiaan voi antaa arvosanan suoraan sillä perusteella, kuinka paljon niillä on määräysvaltaa laskennallisen voimakertoimen suhteen. Jos kaikkien pyörien hyötysuhde on 0,8, saadaan termien arvoiksi 0,8:n potensseja tähän malliin (sininen rivi):

Ja näitä arvoja ynnäämällähän laskennallinen voimakerroin muodostuu. Jos vaikka kyseessä olisi neljän pyörän (edelleen 0,8) "V on V on V on V", jossa yhteen siis lasketaan kaikki 16 termiä, kumulatiivinen summa olisi tällainen (vihreä rivi):

Nollannen ja ensimmäisen asteen termit ovat siis vastuussa 40%:sta kokonaisuudesta, kolmannen ja neljännen alle 25%.

Tässä on muutaman neljän pyörän taljan termit. Pyörien numerointi on kuten yllä tai yleensä niin että P1 on lähinnä kuormaa ja siitä vetävää elementtiä kohti P2 jne.

Ja tässä laskennalliset sekä ideaalit voimakertoimet ja niiden keskinäiset suhteet eli laskennalliset hyötysuhteet, kun köysipyörien hyötysuhde on 0,8:

	Calculated MA	Ideal MA	Calculated efficiency
Simple 5:1	3.36	5.00	0.67
V on V on V on V	10.50	16.00	0.66
Z on Z	5.95	9.00	0.66
11:1	7.11	11.00	0.65

11:1 ja 9:1 välillä on erona kaksi kolmannen asteen termiä, jotka siis tuovat kasvattavat voimakerrointa yhdellä toisen asteen ja yhdellä kolmannen asteen termillä eli summalla 0,64+0,51 = 1,15. Kokonaisuuden hyötysuhdetta tämä ei juuri laske, sillä 9:1:n termit eivät ole oleellisesti tätä parempia eli pienempää astetta.

Jos laskennallisen hyötysuhteen yksitoikkoisuus häiritsee, voi kokeeksi vaihtaa P1:n hyötysuhteeksi 0,3, mikä vastaisi sitä että on I'D tai vastaava PCD:nä:

	Calculated MA	Ideal MA	Calculated efficiency
Simple 5:1	3.11	5.00	0.68
V on V on V on V	7.58	16.00	0.47
Z on Z	4.98	9.00	0.55
11:1	5.41	11.00	0.49

Mukavasti tuli näkyville, että 11:1:ssä kaksi lisärastia Z on Z:aan verrattuna ovat termeissä, joissa on P1 mukana: sen hyötysuhde putosi 16%-yksikköä ja jälkimmäisen 11%-yksikköä. Toiseksi huomataan, ettei yksinkertainen talja paljoa hätkähtänyt. Tahmea PCD vaikuttaa ainoastaan neljännen asteen termiin. Lopputulos on ikään kuin yksinkertainen 4:1, joka juuri ja juuri jaksaa samalla vetää löysät pois PCD:n läpi. Jos käytettävissä on kolme hyvää pyörää ja apukäsiä, voi rakentaa kolmella pyörällä ulkosen taljan (kuten crevasse, 0,8:n pyörillä 3,88:1) ja antaa apulaisen vetää löysät pois PCD:stä. Toisaalta jos apulainenkin tulee vetämään taljaa, tulee pienempi hyötysuhde kompensoitua ja saadaan kaksinkertainen resetointiväli. Samalla homma pysyy paljon yksinkertaisempana (sic). Eipä siis ihme, että pelastus- ja muut köysityöskentelyn ammattilaiset turvautuvat usein yksinkertaisiin taljoihin.

Tässä viitatun yksinkertaisen 5:1:n määritelmä 

Pieni sivupolku, kun nyt kerran yksinkertaisista taljoista tuli puhe: Jos käytetään samanlaisia köysipyöriä, suuntaa vaihtamattoman yksinkertaisen taljan voimakerroin on 1 + P + P^2 + P^3 + ... + P^N, missä N on pyörien määrä. Summan termien sarja kuuluu geometristen sarjojen joukkoon. Voidaan osoittaa, että sarjan summa on 1/(1-P), kunhan P ei ole 1 - ja sehän on valitettavan vääjäämättä totta. Tästä seuraa, että voidaan laskea suurin voimakerroin, joka yksinkertaisella taljalla ikinä voidaan saavuttaa riippumatta siitä, kuinka monta pyörää taljaan käytetään. Nimittäin sarjan summa on sama kuin äärettömästä määrästä pyöriä rakennetun yksinkertaisen taljan laskennallinen voimakerroin.

Esimerkiksi aiemmin käytetyllä hyvällä pyörän hyötysuhteella 0,8 saadaan 1/(1-0,8) = 5. Syvimmät pahoitteluni, mutta tämän suurempaa laskennallista voimakerrointa ei kannata odottaa, sillä jo tämä vaatisi äärettömän määrän pyöriä. Entäpä 0,9? 1/(1-0,9) = 10. Alla olevassa kuvassa näkyy sinisellä voimakertoimen kasvu 0,8:n tapauksessa. Punainen suora on ideaali, usein liian todelliseksi oletettu voimakertoimen kasvu. Nähdään, kuinka olematon lisäys viidennen pyörän paikkeilla saadaan (0,8^5 = 0,32), ja siitä eteenpäin koko ajan pienempi, niin että käyrä todellakin lähestyy arvoa viisi muttei koskaan saavuta sitä.

Yksinkertaisen taljan laskennallinen voimakerroin pyörän hyötysuhteella 0,8, kun on N pyörää. Summa lähestyy viittä, kuten osoitettiin.

Tutkitaan vielä muutamia neljän pyörän taljoja. Otetaan joukko crevasse-taljan variaatioita, jotka saadaan korvaamalla Z-rigin tarraimen ja kättä lähinnä olevan pyörän kytkös erilaisilla "sisäisillä taljoilla".

Crevasse-variaatioiden pohja

Kun X:n tilalla on 1:1-talja eli kiinteä kytkös, saadaan Z-rig. Aiemmin esitelty crevasse saadaan korvaamalla X 2:1-taljalla, joka käyttää ankkurinaan samaa G-elementtiä kuin missä P1 on kiinni. Toinen vaihtoehto ankkuroinnille on elementti E2, ainoa alaspäin liikkuva eli negatiivinen elementti. En edes yritä osoittaa asiaa muodollisesti, mutta ylöspäin liikkuvaan elementtiin ankkuroiminen johtaisi ikävyyksiin voima-analyysin kannalta ja etenkin tyhmiin taljoihin.

Siispä korvataan X erilaisilla kahden pyörän taljoilla käyttämällä ankkurina G:tä ja E2:ta:

Voima-analyysistä saadaan termit:

Jos kaikki pyörät ovat samanlaisia, riittää että lasketaan kunkinasteisten termien määrät:

Koska taljojen ideaalit voimakertoimet vaihtelevat, normalisoidaan vielä nämä lukemat jakamalla ne ko. taljan ideaaleilla voimakertoimilla. Silloin kukin luku kertoo sen, kuinka iso osuus voimakertoimesta on kunkin asteluvun termien harteilla:

Nähdään, että B:n ja F:n kertoimet painottuvat kohti isompia astelukua kun taas A:n ja C:n kohdalla pienemmät asteluvut ovat vahvemmin edustettuina. Sopivasti järjesteltynä saadaan tällainen kuvaaja: 

Astelukujen 0, 1, 2, 3 ja 4 termien osuus taljojen voimakertoimista

Etenkin ensimmäisen ja kolmannen asteen termien painokertoimien peilikuvamaisuus hivelee silmää. Järjestyksessä B-F-E-D-A-C näyttäisi olevan jotain merkittävää. Ja todellakin, B ja F ovat taljoja joissa käytetään X:n ankkurina pelkästään elementtiä E2, E:ssä ja D:ssä sekä E2:ta että G:tä ja A:ssa ja C:ssä pelkkää G:tä. Onhan ihan ymmärrettävää, että jos X ei vedä ankkuria alaspäin vaan jotain taljan liikkuvaa elementtiä, saadaan energian reittejä, jotka kulkevat lisäksi jonkin negatiivisessa suunnassa olevan köysipyörän läpi - tässä tapauksessa P1:n. Sama näkyi jo 9:1 ja 11:1 välillä, niissähän erona oli kaksi termiä joissa molemmissa oli P1.

Normalisoidaan lisää. Tutkitaan näiden lukujen sijasta sitä, kuinka hallitsevia ne ovat omassa ryhmässään, siis kaikkien taljojen samanasteisten termien joukossa. Toisin sanoen lasketaan kunkin asteluvun N palkit yhteen ja jaetaan kukin palkki summalla.

Kunkin taljan N:nnen asteen termien määrän osuus kaikista N:nnen asteen termien määristä 

Tämä on sikäli hieman epätyydyttävä tapa, että arvot riippuvat verrokkitaljoista; käyrät mittaavat taljojen omijaisuuksia suhteessa joukkoon muita. Kokeillaan vielä paria visualisointitapaa joissa tätä heikkoutta ei ole. Toisen asteen termejä on ymmärrettävästi eniten, koska niiden mahdollisia variantteja on eniten. Jaetaan luvut vielä kyseisen asteluvun termien maksimimäärällä (1, 4, 6, 4, 1):

Taljojen kunkin asteluvun termien osuus maksimimäärästä

Nollannen asteen termit eivät ole tässä kovin kiinnostavia, koska kaikilla taljoilla on niitä 1/1. Ensimmäisen asteen mukaan taljat jakautuvat kahteen ryhmään A+B ja loput niin, että A:lla ja B:llä on kaksi neljästä toisen asteen termistä ja muilla kolme. Tämäkään ei tunnu korreloivan aiempien havaintojen kanssa. Sen sijaan toisesta asteesta alkaen tendenssi on selvä: F, E ja B valtaavat kuvaajan yläosan kun D, C ja A painuvat kiltisti nollille. No, neljännessä asteessa vaihtoehtoja on taas tasan kaksi - 1 ja 0 - mutta toisaalta kolmannen asteen termien määrä korreloi tämän kanssa ryhdikkäästi. Niillä, joilla on neljännen asteen termi on kolme tai neljä kolmannen asteen termiä neljästä mahdollisesta ja niillä joilla ei ole neljännen asteen termiä on yksi tai kaksi kolmannen asteen termiä.

Otetaan vielä mukaan kunkin asteluvun kyky todella lisätä voimaa. Sehän riippuu köysipyörien hyötysuhteista: ideaalisessa tilanteessa jokaisen asteluvun jokainen termi tuottaa ykkösen verran voimakerrointa, mutta todellisilla köysipyörillä lisäkerroin pienenee asteluvun kasvaessa. Esimerkiksi 0,8:lla 1, 0,8, 0,64 jne. Tässä 1,0, 0,8:n ja 0,5:n tapaukset:

Efektiivisen voimaertoimen jakautuminen termien asteluvuittain, köysipyörän hyötysuhteena 1

Efektiivisen voimaertoimen jakautuminen termien asteluvuittain, köysipyörän hyötysuhteena 0,8

Efektiivisen voimaertoimen jakautuminen termien asteluvuittain, köysipyörän hyötysuhteena 0,5

Kerroin on karkeasti ottaen sama kuin käyrän alle jäävä pinta-ala. Nähdään, miten oikealle voimistuen painottuva termien efektiivinen teho notkauttaa korkean asteen termit miltei käyttökelvottomiksi.

Lopetetaanpa tämä viisu peräti aavistuksen käytännölliseen nuottiin. Lopun taljavariaatioista A poikkeaa muista tolkullisella ideaalilla voimakertoimellaan (7:1) ja suhteellisen hyvällä suorituskyvyllä. Verrataanpa sitä toiseen ideaalisti 7:1-taljaan, ainakin Petzlin ihan käytännössä suosittelemaan "double marineriin".

Vasemmalla "A", oikealla "double mariner"

A:lla on heti kärkeen pari etua, jotka liittyvät ankkurointiin. Marinerissa kaikki kuorma on P1:n varassa (poislukien vetävä elementti), kun taas A:ssa voidaan jakaa kuormaa kahdelle ankkuripisteelle P1:n ja P3:n kesken. Tähän liittyy myös se, että marinerissa suurempi voima kiskoo köyttä P1:n läpi, mikä näkyy A:ta useampana P1:n sisältävänä terminä. Marinerissa on tietenkin yksi köysipyörä vähemmän, mutta sen voi silti esittää neljän köysipyörän taulukossa - P4 ei vain esiinny kertaakaan:

Yksi käytännöllinen etu on siinä, että A:ssa on vain yksi tarrain ja siis vähemmän huolta resetoinnista. Kun A resetoidaan, P2 ja P4 ovat kosketuksissa. Seuraava resetointi tarvitaan, kun P2 koskettaa P1:tä. Koska P3 ja P4 muodostavat 3:1-taljan, tämä tapahtuu kun P4 ja siis myös taakka on noussut 1/3 P3:n ja P4:n alkuperäisestä välimatkasta eli taljan kokonaispituudesta.

A ja "double mariner" resetoituina, taljan pituus on T. Törmäyksen aiheuttavien osien liikkeet on merkitty katkoviivoilla.

Mariner taas resetoidaan niin, että P2 ja P3 koskettavat ja sisäisen taljan (sininen) yläpään tarrain koskettaa P1:tä. Täällä esiteltyä menetelmää käyttämällä saadaan P2:n nopeudeksi 3S ja tarraimen nopeudeksi -S, kun S on taakan nopeus. Toisin sanoen P2 ja tarrain kohtaavat kun tarrain on tullut 1/4T alaspäin ja P2 3/4T ylöspäin, missä T on taljan alkuperäinen pituus. Ja koska P2 ehtii liikkua nopeudella 3S matkan 3/4T, taakka ehtii liikkua 1/4T.

Siispä paitsi että marineria pitää resetoida kahdesta kohdasta, sitä on resetoitava 1/3 useammin kuin A:ta (jos taljat ovat resetoituina yhtä pitkät) - siis neljä kertaa siinä missä A:ta kolme. Todellisuudessa tällaisia kahdesta kohdasta resetoitavia taljoja todennäköisesti käytetään niin, että kriittisempää (tässä tapauksessa ylempi tarrain) resetoidaan tiheästi ja toista aina silloin kun ensimmäisen resetointiväli menee naurettavan lyhyeksi.

Vertaillaanpa laskennallisia voimakertoimia. Koska molemmilla on kutakin astetta olevia termejä yhtä paljon, samanlaisia köysipyöriä käyttämällä ei tule eroa. Esimerkiksi 0,8:n köysipyörillä molemmat ovat 5,03:1. Tämä on sikäli marinerille epäreilu vertailu, että on huomattavasti epätodennäköisempää saada haalittua kasaan neljä kuin kolme tällaista pyörää. A on vähiten herkkä P1:n hyötysuhteelle, ja sen korvaaminen sulkurenkaalla (0,5) pudottaisi laskennallisen voimakertoimen siedettävään 4,8:1:een. Hyväksyn vastalauseen: PCD:tä ei välttämättä ole helppoa korvata sulkurenkaalla.

Mutta PCD:istä puheen ollen, entäpä jos P1 onkin oikein tahmea kuten grigri tai ATC guide-moodissa? Ja entäpä jos monimutkaista taljaa tarvitaan juuri siksi, että ei ole ensimmäistäkään oikeaa köysipyörää mukana mutta on hätätilassa saatava hinattua yksin kaveri railosta? Kokeillaanpa niin että P1 on 0,3 ja muut 0,5. Mariner: 2,65:1, A: 2,78:1. Eipä tuolla erolla juuri ole merkitystä, mutta siksipä juuri A:n muut edut ovat todellisia etuja.

Entäpä jos on yksi 0,8 köysipyörä käytettävissä? Marinerissa ei ole merkitystä korvaako P2:n vai P3:n, lopputulos on joka tapauksessa 3,21:1. A:ssa kannattaa tässä tapauksessa parantaa P4:n laatua, jolloin saadaan 3,45:1.

Olipa yllättävää löytää jotain potentiaalisesti käytännöllistä teorian kautta. Mielenkiintoista päästä kokeilemaan!

Ankkureista ja kuorman jakamisesta

Jos ankkuri käyttää useampaa pistettä, yksi sen tehtävistä on kuulemma jakaa voima hallitusti pisteiden välillä. Equalisation on ensimmäinen e-kirjain John Longin kylvämässä muistisäännössä SRENE, kun vasta toinen tulee sanaparista No Extension.

Miten ankkurit sitten hoitavat tämän homman? Riippunee ankkurista. Useamman pisteen ankkurien perustyypit voisivat olla kiinteästi tasapainotettu ja itsetasapainottava (ainakaan ensimmäinen ei ole yleisessä käytössä).

Toinen ulottuvuus on pisteiden määrä. En ainakaan itse tiedä mitään käytännöllistä itsetasapainottavaa ankkurityyppiä, joka tasapainottaisi enemmän kuin kaksi pistettä. Sen sijaan yhdistämällä aina kaksi pistettä uudeksi pisteeksi voi rakennella niin monitasoisia itsetasapainottavia härveleitä kuin kehtaa. Yleensä ottaen tässä kirjoitelmassa käsitellään vähintään kahden pisteen ankkureita, vaikkei erikseen aina muistettaisi mainita.

Pisteiden kokema voima riippuu ankkurin geometriasta, eikä niiden summa tarkkaan ottaen koskaan ole sama kuin ankkurin kokema voima. Tämä johtuu ihan vain trigonometriasta ja siitä, että ankkuri muodostaa aina jonkinlaisen kolmion tai useita. Klassinen esimerkki on kaksi pistettä yhdistävä ankkuri, joka 120º kulmalla jakelee kumpaankin pisteeseen saman voiman kuin mikä ankkurin master pointissa on. Suuremmat kulmat tuottavat vielä suurempia voimakertoimia aina 180º teoreettiseen äärettömään asti. Pienemmät toki pienempiä, niin että 60º kulmalla saadaan jo lähes puolitettua kokonaiskuorma, eli ylimääräistä voimaa ei ilmesty paljonkaan.

Mutta onko tässä kaikki? No ei. John Long huomauttaa klassikkokirjassaan, miten eri mittaiset "jalat" joustavat eri lailla. Jos samasta materiaalista leikataan kaksi pätkää, joita toinen on pituudeltaan kaksinkertainen toiseen verrattuna, tämän pidemmän jousivakio on puolet lyhemmän jousivakiosta. Siispä jos molempia vedetään vaikka 10 mm pidemmiksi, lyhempi vaatii kaksinkertaisen voiman. Sehän on sikäli ihan ymmärrettävää, että suhteessa pätkän omaan pituuteen tämä pituuden lisäys on lyhemmällä kaksinkertainen pidempään verrattuna. Toki kuvan kahden pisteen ankkureissa tämä on siedettävää, koska tarvittaisiin aika iso pituusero kokonaan sotkemaan tasapainottaminen.

Edelleen, jos materiaalit eivät olekaan samat, saatetaan törmätä vastaaviin yllätyksiin. Eri materiaaliksi kannattaa tässä suhteessa laskea myös solmittu ja solmimaton materiaali, sillä kaikki solmut antavat periksi kiristyessään, ja solmut kiristyvät kunnes materiaali katkeaa. Seuraavassa kuvassa näkyy pieni koe viime syksyltä. Kootenay on lukittu kiinni, joten siihen pitää suhtautua kuin pollariin tai tolppaan: siinä on siis kiinteä alumiinirumpu ja rummun ja köyden välissä normaali kitka. Oikeanpuolisessa jalassa on alppiperhonen. Tasapainottaako systeemi vinssin voiman kauimmaisina oleville pulteille?

No kyllä, mutta ei kovin täydellisesti. Kiristin yhteensä kuusi kertaa (vaihtelevasti 1000-1500N solmuttomalle puolelle) solmun puolta kolmen kerran jälkeen vaihtaen ja luonnollisesti joka välissä solmu avaten. Solmullinen puoli koki keskimäärin 83% solmuttoman puolen voimasta - pisteiden prosenttiosuuksina kokonasvoimasta ilmaistuna 45-55. Tässä kannattaa muistaa, että kuvioon oli sotkettu kaksi kompaa: pollarin tasapainottavan ominaisuuden näennäisyys ja venyvä solmu. Jos ankkuri olisi ollut kokonaan tasapainottamaton, tulos olisi voinut olla vielä heikompi.

Toinen esimerkki samasta teemasta: Ankkuri on tehty laittamalla solmittu nauha- tai köysilenkki "bucket"-tyyliin palkin ympäri.

Palkki ja solmittu lenkki "bucket"-moodissa

Mistä ankkuri pettää? Todennäköisesti kuvassa oikeata puolelta, joko sulkurenkaan tai palkin takanurkan kohdalta, sieltä missä lenkki on kovimmassa rasituksessa. Solmu toki on lenkin heikoin kohta, mutta samalla se helposti vähentää lenkissä sen puolella olevaa voimaa samassa suhteessa. Itselläni on tästä hieman käytännön kokemusta, mutta tietenkään tätä ei voi ottaa puhtaana faktana. Ennemmin niin, ettei ole ollenkaan varmaa että ankkuri pettäisi solmusta - vaikka solmu tavallaan määrittääkin lujuuden, koska solmun löysäilyn takia muut osat joutuvat kantamaan ylisuuren osuuden kuormasta.

Palataan geometriaan. Vähiten matemaattinen ja siksi ehkä käytännöllisin tapa tutkia ankkurin geometrian vaikutusta voimiin on vektorianalyysi. Vektori on siis otus, jolla on suunta ja pituus. Pituus voi tarkoittaa vaikka voiman suuruutta ja suunta vaikutussuuntaa. Jos jakaa eri suuntaiset voimat pysty- ja vaakakomponentteihin, saadaan niistä sikäli yhteismitallisia, että voidaan verrata niitä toisiinsa. Voimien summa on levossa olevan kappaleen tapauksessa erään Newton-nimisen hepun mukaan nolla, ja sama pätee erikseen voimien pysty- ja vaakakomponentteihin.

Kuvan voimien suuruudet on vedetty hatusta, mutta toivottavasti idea on selvä. Violetit nuolet ovat voimien pystykomponentteja. Kuormassa, voimassa F ei muuta olekaan. Sen sijaan ankkuripisteiden voimat (F1 ja F2) ovat väkisinkin ankkurin jalkojen suuntaiset, koska taipuisalla materiaalilla ei juuri voi kuin vetää. Nämä (mustat) voimat on jaettu violetteihin pysty- ja vihreisiin vaakakomponentteihin Fy ja Fx. Mustan nuolen on siis oltava violetin ja vihreän nuolen virittämän suorakulmion lävistäjä. Vihreiden nuolten on oltava yhtä pitkät, jotta ne suunnaltaan vastakkaisina (ja ainoina vaakasuuntaisina voimina) kumoaisivat toisensa, Fx1 = Fx2.

Siirretään F1 ja F2 päällekkäin niin että F1 on käännetty peilikuvaksi (meitä kiinnostaa lähinnä pituus, ei absoluuttinen suunta):

Mielestäni tämä kuvastaa aika hyvin sitä, miten jalan ja kuormituksen suunnan välinen kulma määrää jalan voiman - mutta vain suhteessa toisten jalkojen voimiin. Fx:n ja Fy:n pituuksista tiedettiin kyllä että ne ovat samat, mutta vektorin pituus oli vedetty hatusta - palataan tähän. Voimien suhde eli se, kuinka ankkuri jakaa kuorman, on kuitenkin selvitettävissä jo tästä kuvasta. Trigonometriaa muistelemalla voi päätyä jopa siihen, että

sin(αi) = Fx/Fi eli Fi = Fx/sin(αi)

missä Fx = Fx1 = Fx2, Fi on vuoroin F1 ja F2 ja αi on vastaavasti kyseistä voimaa vastaava kulma. Tämän voi ilmaista myös niin, että kahden pisteen ankkuri jakaa voiman suhteessa

F1/F2 = sin(α2)/sin(α1)

Esimerkiksi jos toisen jalan kulma on 45º ja toisen 30º, voima jakautuu suhteessa 0,5/0,71.  Siis 30º jalka kantaa 0,71 yksikköä ja 45º jalka 0,5 yksikköä, prosentteina 59-41.

Entä voimien suuruudet? Skaalataan kaikkia ankkurivoimia kuvaavia nuolia niin, että y-komponentit kumoavat kuorman: F = Fy1 + Fy2. Tai vähän matemaattisemmin ilmaistuna:

F = cos(α1)F1 +  cos(α2)F2

Toisin sanoen ankkurin jalan kulmien suhteet määräävät voimien jakautumisen. Voimien absoluuttiseen suuruuden määrää kulmien yleinen taso. Tyyliin:

• Kaksi pientä kulmaa: molemmissa pieni voima
• Pieni ja iso kulma: pienessä keskikokoinen voima, isossa pieni
• Kaksi isoa kulmaa: molemmissa iso voima.

Itselleni tämä oli hieman työlästä ymmärtää, koska köysiratafysiikan pauloissa unohdin hyväksi aikaa mahdollisuuden että suuressa kulmassa oleva ankkurin jalka voisi päästä vähällä. Siis vain sikäli vaakatasossa oleva köysirata, että kumpikin kulmista on suuri, tuottaa molempiin ankkureihin suuren kuorman.

No kiva, mutta entä jos pisteitä on useita?

Seuraa kaksi ongelmaa, jotka oikeastaan pohjimmiltaan ovat yksi ja sama asia. Tällaista tilannetta kuvataan statiikassa (joka on fysiikan, tarkemmin mekaniikan osa-alue) staattisesti määräämättömäksi rakenteeksi. Englanniksi puhutaan paljastavasti redundanssista. Rakenne on ylimääritelty; jo kaksi jalkaa riittää tasotapauksessa määräämään ankkurin muodon, kolmas on matemaattisesti hankala koska sen pituus ei ole vapaa muuttuja vaan se määräytyy kahden muun perusteella.

Mekaniikassa tämän ratkaisemiseen on keinonsa joihin en tässä mene, mutta ongelma heijastuu myös oikeaan elämään. Kun nimittäin äskeiseen kahden pisteen systeemiin lisätään kolmas jalka, oikeastikin on pidettävä itse huoli että sen pituus sopii yhteen kahden aikaisemman kanssa. Jos yksi jalka on liian pitkä tarvittavaan nähden, se ei kanna yhtään voimaa. On tietenkin mahdotonta mitoittaa kaikki jalat täysin oikein, mutta onneksi oikean elämän asiat joustavat.

Olen jopa hieman mittaillut, kuinka paljon. Esimerkiksi jos puoli metriä pitkä ankkurin jalka koostuu kaksinkertaisesta 6 mm narusta, sen jousivakio saattaa olla vaikka 120 kN/m eli 0,12 kN/mm. Siispä jokaista jalan pituuden 1 mm virhettä kohden jalan voima vaihtuu 0,12 kN ja yhtä senttimetriä kohden 1,2 kN. Joustaminen siis toki auttaa jakamaan kuormaa pisteille, mutta totta kai eniten joustamaan joutuvat saavat vääristyneen osuuden kuormasta.

Palataan hetkeksi sivusuuntaisiin voimiin. Staattisen määräämättömyyden ongelma näkyy siinä, että kun sivusuuntaisia voimia on enemmän kuin kaksi, ei voi yksinkertaisesti päätellä että ne ovat yhtä suuret ja suunniltaan vastakkaiset. Jos pisteitä on kolme, käytännössä aina on kaksi yhteen suuntaan ja kolmas niiden kanssa vastakkaiseen, eikä mistään voi tietää, kuinka ne jakautuvat. Sen sijaan sen voi kyllä päätellä, että kaksi samaan suuntaan vetävää pistettä pääsee paljon vähemmällä, koska kolmannen vaakasuuntainen komponentti joutuu yksin kumoamaan kahden muun pisteen vaakasuuntaiset komponentit. Tuo ylläoleva kuva on muuten hyvä, mutta olisi pitänyt piirtää oikean puolen vihreä nuoli vielä pidemmäksi - ja sitä kautta oikean puolen mustakin nuoli. Ja onhan se tietenkin ihan loogista, etenkin jos ajattelee että vasemman puolen kaksi jalkaa olisivat syntyneet jakamalla yksi jalka kahdeksi.

Siis jos ankkuri on tasapainotettu joten kuten, jokainen jalka kyllä saa osakseen jonkin kuorman, kunhan ankkuria kuormitetaan ja siis jalat venyvät tarpeeksi. Tutkitaanpa jalkojen venymistä. Kun ankkuri venyy ja kuorma siirtyy alaspäin pienen matkan dK, erilaisista trigonometristen funktioden derivaattoihin liittyvistä seikoista johtuen ankkurin jalka venyy cos2(α) * dK, missä cos2 tarkoittaa kosinin toista potenssia ja α on edelleen jalan ja kuormituksen suunnan välinen kulma.

Jos ankkurin pisteet ovat samalla korkeudella, jalan pituus on x/cos(α), jossa x on ankkurin korkeus (eli 0-kulmassa olevan jalan pituus).

Jos jalat lisäksi ovat samaa materiaalia, kunkin jousivakio on suhteessa pituuden käänteislukuun. Pituus taas oli x/cos(α), joten jousivakio on suoraan verrannollinen cos(α):aan. Sanotaan että jousivakio on k*cos(α). Kun ankkuri taas kuormittuessaan venyy matkan dK, jolloin siis kunkin jalan pituus kasvaa cos2(α)dK, ja tällä pituuden kasvulla saadaan voiman muutos cos2(α)dK * k * cos(α) =

cos3(α)* k * dK 

jossa cos3(α) tarkoittaa kosinin kolmatta potenssia. Suomeksi: kuvan ankkurin reunimmaiset jalat saavat osakseen 0,6 - 0,9 kertaa (kuvitellun) 0-kulmassa olevan jalan kuorman. Cos3(30º) on noin 0,6 ja cos3(15º) on noin 0,9.

Vastaavat prosenttiosuudet pisteiden kuormille ovat 27-46-27 (30º) ja 32-36-32 (15º). 15º tapaus ei siis todellakaan ole huono - siispä pieni ankkurikulmako on hyvä asia? (Muistutetaan tässä, että α oli yhden jalan ja kuormituksen suunnan välinen kulma, joten symmetrisen ankkurin kokonaiskulma olisi kaksinkertainan)

Jos kuormituksen suunta jostain syystä vaihtelee tai on eri kuin oletettiin, mikä on vaikutus kuorman jakautumiseen? Tutkitaan kahden pisteen symmetristä, kiinteästi tasapainotettua ankkuria. Kummankin jalan kulma on α, joten ankkurin kokonaiskulma on 2α. Tähän symmetriaan nähden ankkurin kokema kuormitus onkin yllättäen kulman ꞵ verran kallellaan:

On helppoa nähdä, että tämä olisi täsmälleen sama asia kuin ankkurin jalkojen kulmien epäsymmetria (α+ꞵ, α-ꞵ). Voimat jakautuisivat siis suhteessa FA/FB = sin(α+ꞵ)/sin(α-ꞵ). Jos α=ꞵ eli kuorma on samansuuntainen kuin toinen jalka, tässä tapauksessa A, nimittäjän sin(α-ꞵ) = sin(0) = 0 aiheuttaa ongelmia: suhde lähestyy ääretöntä. No, se tarkoittaa vain että A kantaa 100% lähestyvän osuuden ja B nollaa lähestyvän. Ja tämähän on selvää ilman matematiikkaakin: jos kuorma on A-jalan suuntainen, B ei tee juurikaan mitään.

Selväähän on, että mitä pienempi kulma, sen pienemmällä arviointivirheellä tähän tilanteeseen joudutaan - ja ylipäätään sitä herkempi ankkuripisteiden tasapaino on kuormituksen suunnan vaihteluille.

Jos vielä todetaan, että sin(a)/sin(b) ≈ a/b, voidaan päätellä että myös kulmien ja sitä kautta pisteiden väliin tällä tavalla viritettyjen kaarten pituuksien suhde kuvastaa voimien jakautumista ankkuripisteille:

Voi siis ajatella, että kuormituksen suunta toimii ikään kuin viisarina, joka osoittaa voiman painottumisen. Ja asteikko kaiken lisäksi on lineaarinen, eli mittaamalla kaaren a ja kaaren b pituuksien suhteen saa koko lailla oikean suhteen voimien jakautumisesta B:n ja A:n välillä.

Teoretisoidaanpa loppuun vielä hetki itsetasapainottavien ankkurityyppien kanssa. Niissähän ideana on, että jalat ovat samaa jatkuvaa materiaalia, joka itsekseen asettuu sellaiseen asemaan jossa voimat jakautuvat jalkojen kesken tasan. Ankkurissa on siis yksi tai useampia köysipyöriä, jos sellaiseksi voidaan laskea myös sulkurengas tai mikä tahansa muu joka vastaavan homman jollain lailla hoitaa.

Kuvassa on kaksi pistettä yhdistävä tapaus kaaviomaisesti esitettynä. Tällainen voisi olla vaikka quad tai sliding x. Joskin on sanottava, että sliding x:ssä on asioita jotka tekevät siitä huomattavasti tahmeamman kuin tämä malli. Kuormat pisteiden A ja B välillä eivät siis voi olla erisuuruiset? No eivät, jos köysipyörä hoitaa hommansa ideaalisesti. Ja sehän riippuu ihan köysipyörästä tai sellaisen korvikkeesta, miten se sen tekee.

Jos ankkurissa oikeasti käytetään köysipyörää, voidaan olla melko varmoja että toisella puolella on vähintään 80% toisen puolen kuormasta. Se tarkoittaisi prosenttiosuuksina 56-44 tai parempi. Ei valittamista! Mutta eihän siinä yleensä käytetä, vaan sulkurengasta. Sulkurengas taas toimii köysipyöränä niinkin kehnosti, ettei voi olettaa suhteeksi 50% parempaa, jolloin jakautumisprosentit olisivat tietenkin 67-33. Tämän olen monesti ihan itse mitannut, ja ehkäpä innostun aiheesta oikein kirjoittamaankin.

Redundanssi, varmuuskerroin ja muuta turvallisusmietettä

Kirjoittelenpa ihan omia ajatuksiani selvittääkseni. Sinä, satunnainen lukija, joudut nyt työkalukseni häikäilemättömässä, omaa etuani tavoittelevassa hankkeessa. Nimittäin vaikka kirjoitan näitä itselleni, kuviteltu (ja hyvin pienessä mittakaavassa jopa todellinen) yleisö saa ajattelemaan ja etenkin ilmaisemaan huolellisemmin.

En ole riskienhallinnan osaaja. Tämä pohdiskelu on pelkkää maallikon ihmettelyä. Älä siis usko ollenkaan.

Lentokoneet ja monet kiipeilyyn liittyvät järjestelmät pyritään suunnittelemaan tiettyjen turvallisuuteen tähtäävien periaatteiden mukaan. Järjestelmien ja niiden osien sisäänrakennettua, luontaista turvallisuutta (inherent safety) voidaan yrittää parantaa. Järjestelmiä tai niiden osia voidaan moninkertaistaa eli lisätä redundanssia. Kiipeilyssä harvemmin puhutaan vikaantumisvälistä tai muista tilastollisista vikaantumisen tai virhetoiminnon todennäköisyyttä kuvaavista muuttujista, mutta kylläkin varmuuskertoimista eli oletetun maksimisuorituskyvyn ja  suunnitellun tarpeen välisestä suhteesta. Kiipeilyssä ei myöskään jatkuvasti tehdä riskianalyyseja, mutta se johtunee siitä että valtaosa kiipeilystä on itse asiassa aiemmin suunniteltujen järjestelmien ja kaupallisten tuotteiden käyttämistä.

Järjestelmä on fail-safe, jos sen vikaantuminen ei johda vaaratilanteeseen, vaikka järjestelmä ei enää toimittaisikaan kaikkia funktiotaan. Esimerkiksi junan jarru aukeaa ilmanpaineella, jolloin paineen katoaminen saa junan jarruttamaan. Juna ei aja päin asioita, mutta ei toisaalta enää pysähdettyään lähde liikkeellekään. Petzl Asapilla on tiettyjä samoja piirteitä, mutta eipä se kovin hyvä esimerkki fail-safesta olla. Jos kiipeilyyn liittyviä, todellisia fail-safe -ratkaisuja onkin olemassa, ne taitavat lymytä joidenkin monimutkaisempien teknisten kiipeilyvälineiden sisällä.

On tavallaan kiinnostavaa, että jos kaikki epävarmuustekijät poistettaisiin (kuulostaa vähäpätöisemmältä kuin vaihtoehtoinen ilmaus "jos tiedettäisiin ja osattaisiin ottaa huomioon kaikki maailmankaikkeuden asiat"), niin varmuuskerroin yksi riittäisi. Siis vaikkapa puhuttaessa liimapultin mekaanisesta lujuudesta, jos tiedettäisiin että siihen ikinä klippaavista kiipeilijöistä sejase päivänä ja vuonna tämäjatuo pannuttaa siihen kovimman kuormituksen mitä se ikinä tulee kokemaan, 2,48 kN, pultin lujuudeksi riittäisi 2,48 kN. Toki lujuus tässä tarkoittaisi sitä, että pultti ei rikkoudu 2,48 kN kuormalla mutta 2,48001 kN saa sen rikkoutumaan. Siispä se, että päivänä ja vuonna tämäjatuo pultin päälle ei lisäksi ollut laskeutunut katastrofaalisen 0,00001 kN painovoiman aiheuttava perhonen, ei  olisi ollut sattumaa, eikä siihen sikäli ollut mitään syytä varautua.

Tässäpä jo sujuvasti lipsahdettiin lujuuksiin. Kiipeilytekniikassa varmuutta yritetään kovasti kvantifioida puhumalla lujuudesta. Lujuudella tarkoitetaan yleensä MBS:ää, minimimurtolujuutta, missä on tietyt ongelmansa. Ensinnäkin murtuminen on rikkoutumisen äärimmäinen muoto. Ennen sitä kaikki käyttökelpoiset materiaalit ovat jo myötäneet eli muuttaneet pysyvästi muotoaan. Ja sitä ennen ne ovat muuttaneet muotoaan palautuvasti, elastisesti, siten että kuorman poistaminen palauttaa muodon koko lailla ennalleen. Siipä pitäisi määritellä, mitä edellä tarinoidussa esimerkissä tarkoitetaan "rikkoutumisella". Onko se ensimmäinen hitunen myötämistä, murtuminen vai jotain tältä väliltä?

Toki kiipeilyyn liittyy muitakin kvantifiointikelposia turvallisuuslukuja kuin lujuus, mutta välineiden loppukäyttäjää ei niillä juuri kiusata. Sellaisia voisi olla vaikka Grigrin tai Asapin lukittumisen todennäköisyys kun tehdään jokin standardikoe satoja kertoja, tai vaikka erilaisten virheellisesti sekoitettujen tai vanhentuneiden pulttiliimojen kuivuminen.

Minkä sorttisia tuntemattomia maailmassa on, jos nyt keskitytään kiipeilyvälineisiin ja erityisesti lujuuteen?

• Kuormitus
• Materiaalin ominaisuudet, vaihtelu yksilöiden ja sarjojen välillä
• Välineisiin käytön myötä tulleet kolhut, ruoste jne.
• Inhimillinen virhe, väärinkäyttö

Kuormitus liittyy suunniteltuun normaaliin käyttöön. Esimerkiksi liimapultin normaalin käytön aiheuttama kuormitus varmaankin määräytyy sen mukaan, mikä on suurin voima mitä suuri joukko kiipeilijöitä onnistuu monta kertaa pultin varaan putoillessaan siihen kohdistamaan. Laskeutumislaitteen normaali käyttö määräytyy "normaalin" laskeutujan painoskaalan ylärajan mukaan niin että mukana on tilaa myös "normaaleille" töyssyille. Eli jälleen se, mitä suuri joukko "normaaleja" käyttötapahtumia maksimissaan tuottaisi.

Materiaalin ja muiden laiteyksilöiden välillä vaihtelevien asioiden tutkiminen on taas yksi kiinnostava juttu. Kun nimittäin lujuus on helppoa mitata suoraan (kunhan se on ensin määritelty, ja määritteleminen on suhteellisen yksinkertaista), mutta se tapahtuu rikkomalla tutkittava laite. Tilanne muistuttaa hölmöläisten tulitikkujen testaamista: vain polttamalla kaikki voi täysin varmasti päätellä, että kaikki olivat toimivia. Jos polttaa vaikka kymmenen sadasta, saa hyvää osviittaa, mutta mikä tai mitkä tahasa lopuista 90 tikusta saattavat olla toimimattomia. Tervetuloa, tilastotiede.

Upean tilastomatematiikan (ja sen valtavan käyttökokemuksen) ansiosta osataan hyvinkin päätellä, kuinka suurilla näytemäärillä päästään millaiseenkin todennäköisyyteen, että joukossa on toimimaton tikku. Kun lisäksi valjastetaan valtava kokemus esimerkiksi alumiinin materiaalimekaniikasta ja takomistaidosta, voidaan hyvin tarkasti perustella todennäköisyys sille, että yksittäinen sulkurengas täysin yllättäen olisi ratkaisevast heikompi kuin valtaosa - eli rikkoutuisi pienemmällä voimalla, jos se satuttaisiin rikkomaan ja mittaamaan voima. Oli miten oli, vaikka tämä todennäköisyys puristettaisiin miten pieneksi, se ei koskaan ole nolla (tämä on tilastotieteen sisäänrakennettu ominaisuus). Siispä aina on periaatteessa mahdollista että jostain tupsahtaa uudenkarhea, kaikin puolin normaalin oloinen sulkurengas, joka vain yksinkertaisesti huonon tuurin takia on 50% keskimääräistä heikompi.

Minimimurtolujuus muuten on tilastollinen suure jo sekin. Usein puhutaan kolmen sigman eli kolmen keskihajonnan menetelmästä. Tiedetään, että useimmat maailman satunnaiset asiat noudattavat normaalijakautumaa. Normaalijakautumasta taas tiedetään kokemusperäisesti (ja matemaattisesti), kuinka todennäköinen tietty tutkittavan suureen arvo on, kun tiedetään keskihajonta. Kun erästä sulkurenkaita poimitaan satunnainen sarja murtolujuuskokeeseen ja lasketaan tulosten keskihajonta (kuinka paljon murtolujuus keskimäärin poikkeaa lujuuksien keskiarvosta), voidaan laskea, kuinka epätodennäköistä on saada tiettyä rajaa pienempi lujuus. Kun mainitun koesarjan keskimääräisestä tuloksesta (esim. 27,5 kN) vähennetään keskihajonta (esimerkiksi 0,45 kN) kerrottuna kolmella, saadaan 26,15 kN. Tulos tarkoittaa, että tilastollisesti 99,7% sulkurenkaista on lujempia kuin 26,15 kN ja sulkurenkaan kupeeseen voidaan edelleen leimata 26 kN.

Edelleen sivupolulla; hauska knoppi. Jos itse koeponnistaa yhden tai muutaman kappaleen jotain kiipeilykamaa ja saa selvästi ilmoitettua MBS-arvoa korkeampia tuloksia, pitäisikö olla erityisen tyytyväinen kyseiseen tuotteeseen? Ehkä, onhan se hienoa, jos valmistajalla on varaa ilmoittaa todellista arvoa matalampi kolmen sigman MBS-arvo. Esimerkiksi juuri tuo 26 kN ei jotenkin kuulosta tyylikkäältä, se saatettaisiin jo imagosyistä "pyöristää" 25 tai 24 kN:ksi. Sulkurenkaanhan ei sinänsä tarvitse mennä rikki ollenkaan (kuten sulakkeen), joten lujuutta saa vähätellä niin paljon kuin lystää. Mutta toinen mahdollinen syy on siinä, että annettu matalampi arvo todella on kolmen sigman MBS. Jos näiden sulkurenkaiden lujuus vaihtelee paljon, mikä merkitsee huonoa laatua, keskihajonta kasvaa. Jos sulkurenkaan kolmen sigman MBS on sama 26 kN mutta keskimääräinen MBS (eli todennäköisin tulos yksittäisessä testissä) on 30 kN, voidaan keskihajonnan päätellä olevan 1,3 kN - aika iso vaihtelu. Tai jos viedään ajatusleikki äärimmilleen: jos törmää johonkin laivojen laituriin kiinnittämisen mieleen tuovaan kamaan jossa lukee vaatimattomasti 26 kN, voisiko kyseessä olla aivan katastrofaalisen huono laatu: 200 kN keskiarvo, 58 kN keskihajonta? Arvot heittelisivät niin villisti, että vasta 26 kN kohdalla voisi alkaa olla melko varma ettei kovasti huonompia enää tule vastaan.

Sivupolun perään sivuhuomautus. MBS on siis hyvin epätodennäköisesti laitteen rikkova kuormitus. Tässä pohdiskelussa puhun sujuvasti niin ja niin monen kilonewtonin pisteestä ja sitten varmuuskertoimesta yksi, jos odotettu kuorma on yhtä suuri. En edes osaa ottaa kantaa siihen, tarkoittaako "varmuuskerroin yksi" sitä, että 99,7% tapauksista ei petä.

Välineiden kulumisen aiheuttama heikkeneminen on selkeämpi asia, mutta ei yhtään sen helpompaa mitata - vastaus saadaan taas samalla kun väline rikkoutuu. Tilastollisesti asia on vielä vaikeampi, olettaisin, koska "käytön" kvantifioiminen on lähestulkoon mahdotonta. Ei yksinkertaisesti ole olemassa riittävän suurta määrää käytettyjä kiipeilykamoja, jonka koko historia jokaista kolhua, kemikaaleille ja valolle altistumista jne. myöten olisi tarkasti mitattu ja kirjattu. Ja vaikka tällainen ihmeellinen tilasto jostain saataisiin, ei normaalissa käytössä olevista välineistä kuitenkaan olisi vastaavia tietoja, joten tilasto olisi hyödytön. Metalliset välineet eivät juurikaan heikkene elleivät vaurioidu, mutta esimerkiksi likaantuneet köydet todella menettävät ajan mittaan tuntuvan osan lujuudestaan. Mitä taas metallisiin välineisiin tulee, niiden vaurioitumisen tunnistaminen voi olla todella vaikeaa kokeneellekin, etenkin jos kytössä ei ole ehjää vertailukappaletta.

Siispä on olemassa oikein hyvä syy sille, ettei MBS-arvoja (edes kolmen sigman) oteta sellaisinaan laskelmiin - eli luoteta siihen, että "normaalin käytön" 2,5 kN vaatimus hoituu 2,5 kN MBS-arvon laitteella, vaan oletettua lujuutta verotetaan varulta vähän. Voisi ehkä olla luontevaa analysoida asia juuri näin, siis jakamalla kolmen sigman MBS:ää ykköstä suuremmalla tai kertomalla ykköstä pienemmällä varmuusluvulla, mutta käytännössä onkin tapana kertoa vaadittua lujuutta ykköstä isommalla kertoimella. Esimerkiksi potilasta kannattelevien lääkintälaitteiden on tilanteesta riippuen kestettävä 4-6 kertaa standardipotilaan paino romahtamatta. Siispä tässä tapauksessa voitaisiin kertoa "normaalin käytön" aiheuttama 2,5 kN vaikka neljällä ja saada 10 kN.

Eräs hieman erillinen yhteys, jossa jakamalla MBS ykköstä suuremmalla päästään kuormaan jonka jokin laite varmasti kestää, on WLL (working load limit) tai SWL (safe working limit) eli suurin sallittu käyttökuorma. Lääkintälaitteilla luku (suunnittelukerroin, design factor) on siis 4-6 ja WLL on viranomaisten määräämä standardipotilaan paino. Kiipeilykamoissa WLL annetaan tyypillisesti köysipyörille tai vaikka nykäyksenvaimentimille. Kyseessä on ehkä hieman eri asia kuin turvallisuuteen liittyvä varmuusluku. Esimerkiksi köysipyörille on annettava myös MBS, jota käytetään turvallisuuteen liittyvissä asioissa. Hieman kärjistäen WLL koskee vain laitteen muita funktioita kuin asoiden putoamisen estämistä. Esimerkiksi köysipyörän laakeri saa hajota aivan totaalisesti reilusti ennen MBS:ää, kunhan se ei vaaranna asioiden pysymistä ylhäällä. Tässä kirjoitelmassa WLL-ajatus jää hieman heitteille, vaikkei pitäisi. Onhan toki hyvä pitää huoli paitsi siitä, että laitteiden totaalinen murtuminen on riittävän epätodennäköistä, myös siitä etteivät ne murtumattakaan joudu liian lujille ja esimerkiksi väsymisen kautta vähitellen heikkene.

Oli miten oli, kiipeilyssä on valittu käyttää MBS:ää referenssinä ja sisällyttää epävarmuus kertoimeen, jolla normaalin käytön aiheuttamaa kuormaa kasvatetaan kohti sitä mutta ei toivottavasti yli.

Mutta pitäisikö "normaaliin käyttöön" luottaa sen kummemmin kuin kolmen sigman MBS:ään? Ainahan voi tapahtua jotain täysin yllättävää. Ihmiset painavat yllättävän paljon, putoavat yllättävän suurella putoamiskertoimella, kiviä putoaa, yläpuolella kiipeäviä kiipeilijöitä putoaa, mitähän vielä (sic - jos nämä kaikki osaisi listata, tämänkin tekstin substanssista haihtuisi reilu tussaus). Lisäksi ihmiset tekevät virheitä kytkiessään sulkurenkaita (esimerkiksi portin kuormittaminen) ja tehdessään solmuja, mutta ainakin omassa logiikassani nämä karkeat virheet ovat hieman eri kategoriassa. Vaikka olisikin 0,0001 suuruinen todennäköisyys, ettei kiipeilijä osaa solmia kasia oikein, ei siihen auta mikään varmuuskerroin köyden lujuuden suhteen. Mutta siis pitäisikö myös normaaliin käyttöön ujuttaa erillinen lujuuden varmuuskerroin?

Esimerkiksi teollisuuskiipeilyjärjestö Irata ei näytä näin tekevän. Heidän "raamatussaan" ICoP:ssa eli International Code of Practicessa vain todetaan, ettei kiipeilijän katsota voivan aiheuttaa ankkurille yli 6kN kuormaa. On muuten huomattava, ettei Irata oleta kiipeilijöiden juuri liidaavan, vaan kyse on roikkumisesta semistaattisilla köysillä tai putoamistapauksessa nykäyksenvaimentimen käytöstä. Kun tämä 6kN kerrotaan varmuuskertoimella 2,5, saadaan Iratan erittäin merkittävä 15 kN vaatimus ankkurille.

UIAA ei tietääkseni aseta vastaavia vaatimuksia harrastekiipeilyyn, mutta monessa muussa yhteydessä UIAA:n ja EN:n MBS-vaatimus on tyypillisesti 20-22 kN. Osaksi tätä suurempaa vaatimusta selittää se, että teollisuuskiipeilyssä ankkurijärjestelmä on kaksinkertaistettu. Osaksi varmaan se, että sporttikiipeilyssä "normaalin käytön" kirjo on niin mittava, että kaikkien mitä älyttömämpien yllätysten takia myös sen tuomaa lujuusvaatimusta on järkeilyn sijasta paisutettu sen kummemmin erittelemättömällä varmuuskertoimella. En tiedä onko tätä kerrointa tosiaan koskaan jaoteltu osiin, mutta yhteensähän se näyttää olevan kymmenen luokkaa - tai ainakin huomattavasti enemmän kuin Iratan 2,5.

Iratan 15 kN on luvallista saavuttaa myös yhdistämällä kaksi vähintään 10 kN pistettä. Menetelmäksi yhdistämiseen mainitaan (esimerkiksi) y-hang, joka on kiinteästi tasapainotettu todellakin Y:n muotoinen ankkuri. tasapainottamiselle (equalization) ei anneta kummempia vaatimuksia, paitsi että esimerkkikuvissa Y on symmetrinen ja ankkurikulman maksimiksi asetetaan 90 astetta - tällaisen ankkurin pitäisi tasapainottaa melko hyvin. Olen joskus leikkinyt pienemmän kulman ankkureilla, ja esimerkiksi nylonslingillä tehty sliding x sallii helposti 60-40 -jakautuman pisteiden välille, vaikkei erityisesti yrittäisi asettaa painopistettä vinoon. 70-30 on yllättävän helppoa saada aikaan.

Herää kysymys, onko kahden pisteen käyttämisen tarkoitus vähentää kullekin pisteelle tulevaa kuormaa vai pienentää yksittäisen pisteen varmuuskerrointa ja siis kasvattaa pettämisen todennäköisyyttä sillä varjolla, että kahden pisteen pettäminen on kokonaisuutena epätodennäköisempää? Nämähän ovat oleellisesti eri asiat. Jos varmuuskerroin yhden 15 kN pisteen kohdalla olisi yksi tai vähän alle, ankkuri pettäisi. Jos taas se korvattaisiin kahdella 10 kN pisteellä, ne voisivat hyvinkin kestää, jos tasapainotus sattuisi olemaan tarpeeksi hyvä (kuormitus olisi noin 7,5 kN + 7,5 kN).

Oletan, ettei yksittäisen pisteen kuorman vähentämisellä ole tässä merkitystä. vaadittu 10 kN on kuitenkin selvästi enemmän kuin suurin oletettu käytön aiheuttama kuormitus 6 kN (varmuuskerroin 1,7). Ja koska varalla on toinen 10 kN piste samalla varmuuskertoimella, on oikeastaan melko toivotonta saada molemmat rikki. Todennäköisyyshän toimii niin, että jos tapahtuman A todennäköisyys on P(A) ja tapahtuman B todennäköisyys on P(B), todennäköisyys että molemmat tapahtuvat P(AxB) on P(A)*P(B). Esimerkiksi jos P(A) ja P(B) ovat molemmat 1% eli 0,01, P(AxB) = 0,00001 eli 0,01%. Prosentti prosentista, käyhän se järkeen.

Toisin sanoen oletan, että ankkuripisteen tuplaamisen tarkoitus on pudottaa rikkoutumisen todennköisyyttä:

P(15) ≥ P(10)*P(10),

missä P(N) on todennäköisyys että N kilonewtonin ankkuri pettää. Jos esimerkiksi P(10) = 1% (melko kuumottava, yksi sadasta tapauksesta pettää), P(15) pitäisi olla pienempi kuin 0,01% (1/10000) ettei korvaaminen kahdella 1% ankkurilla olisi tilastollisesti vähintään yhtä hyvä. Eli joko tuplataan tai etsitään sata kertaa niin varma ankkuri - kuulostaa helpolta valinnalta. Tätä moninkertaisuutta siis kutsutaan redundanssiksi.

Mutta toimiiko ankkurin tuplaamisen todennäköosyyslaskenta oikeasti? Ainakin yksi tunnettu ongelma tässä olettamuksessa on: ankkurin piteneminen (extension) yhden pisteen pettäessä. Ilmiö on tuttu rakennusten ja esimerkiksi siltojen lujuuksia tutkiville lujuuslaskijoille ja rakennesuunnittelijoille. Jos vaikka siltaa kannattelee useampi rinnakkainen vaijeri, niin toden totta sillan rakenteessa on redundanssia. Mutta ilmeisesti kukaan ei vielä toistaiseksi ole keksinyt sellaista rakennetta, jossa yhden vaijerin pettäessä muut ottaisivat (vääjäämättä yhtä vaijeria kohti mitattuna kasvavan) kuorman huomaansa ilman minkäänlaista iskukuormaa eli suomeksi rysäystä. Jos rakenne olisi äärettömän jäykkä, tämä kai olisi jossain määrin mahdollista. Todellisen elämän materiaalit venyvät (ja turvallisuuden takia niiltä todella toivotaan sitä, esimerkiksi se aiemmin mainittu lääkintälaitteiden suunnittelukertoimen 4 ja 6 ero johtuu materiaalien murtovenymästä, pienemmällä venymällä murtuvat saavat niskaansa vaativamman kertoimen 6). Ja kun neljän vaijerin sijasta saman sillan painon kantaakin kolme vaijeria, jokaisen kokema kuorma kasvaa 32%, mistä todennäköisesti seuraa vaijerien oleellinen piteneminen ja sillan massan rojahtaminen hieman alaspäin. Jos vaijerien venymä on alun perinkin niin pieni, ettei 32% lisäys aiheuta juuri pitenemistä, vähintään tapauksissa joissa vaikkapa sillan toisen puolen rakenteet pettävät ja toinen puoli (ihan laskelmien mukaan) saa koko sillan kannateltavakseen, on selvää ettei pelkkä kuorman kaksinkertaistaminen riitä laskelmissa, vaan on otettava huomioon romahtamisen aiheuttama iskukuorma. Onhan näitä kokeiltu.

Kiipeilyankkureissa (tai niiden kiinnityspisteiden ja varmistettavan massan välillä) on yleensä jotain suhteellisen joustavaa. Ei aina: oikein staattisesta slingistä tehty sliding x jossa roikutaan suoraan lehmänhännällä voi olla todella kova. Mutta esimerkiksi normaalisti varmistamalla, myös liidatessa, ankkurin piteneminen ei aiheuta juuri ollenkaan putoamiskerrointa. Silti on syytä varautua pahimpaan, ja esimerkiksi trädiankkurissa todellakin saattaa roikkua varmistaja hyvin lyhyellä ja staattisella lehmänhännällä. Ei ole huono oletus, että pitenemisen aiheuttama iskukuorma saattaa esimerkiksi kaksin- tai kolminkertaistaa ankkurin kuorman hetkellisesti.

Toinen ongelma on tasapainottaminen. Asiaa pitäisi tutkia enemmän, mutta hieman voimamittareilla leikittyäni olen saanut käsityksen, ettei edes "itsetasapainottavilta" kannata olettaa yhtään parempaa tasapainotusta kuin 70-30. Onhan se toki huono, mutta ei todellakaan mahdoton ihan järkevänkin näköisissä ankkureissa. Enkä väitä, etteivätkö taitavat ja teknisesti näppärät pääsisi helposti tasaiseen 60-40-tasoon tai parempaan, mutta valitettavasti yleisiä linjoja vetäessä ei ole mitään merkitystä sillä mitä parhaat osaavat.

Leikitäänpä sellaisella ajatuksella, että haluttaisiin kytkeä kolme luonnollista varmistusvälinettä hienolla itse tasapainottavalla systeemillä, kuten esimerkiksi John Longin kirjassa Climbing Anchors tehdään. Koska yksi piisseistä on vähän kiikkerämpi pieni kiila, yritetään jyvittää sille vähän vähemmän kuormaa kuin systeemin lämpimimmän tunteen antavalle isolle liikkuvaleukaiselle. Alla on kaavio, jossa A on vahvin piissi ja C se jännittävä.

Jos nyt oletetaan, että punainen ja sininen alisysteemi (vaikka sliding x:iä) tasapainottavat 70-30, 30-70 tai jotain siltä väliltä, voidaan selvittää ääritapaukset A:n, B:n ja C:n kokemille kuormille. B ja C ovat sikäli symmetrisiä tapauksia, ettei niiden välillä oleteta olevan eroa tässä. Päädytään seuraaviin kuormaskaaloihin:

A: 0,3F ...0,7F
B ja C: 0,1F ... 0,5F

Siis huonoimmassa tapauksessa C:n kannalta molemmissa alisysteemeissä 70% kuormasta sattuu menemään oikealle, jolloin C kokee 0,7*0,7F = 0,5F. Toki tämä on samalla tavalla epätodennäköistä kuin kahden ankkuripisteen pettäminen, mutta silti on tärkeää ymmärtää, ettei ankkuripisteiden kokemien voimien jakaminen ole niin täsmällistä puuhaa kuin saattaisi sohvalta käsin ja voimamittareita koskaan kokeilematta luulla. Otetaan vielä pieni empiirinen esimerkki (siitä voi sitten keskustella, onko tämä oikeaa elämää). Asettelin kolme voimamittaria roikkumaan niin, että kun niitä käyttää pisteinä rakentaakseen n. 250 cm pitkällä lenkillä solmitun cordeletteankkurin, reunimmaisten pisteiden väliseksi kulmaksi tulee 45º. Pisteet olivat melko samassa tasossa ja reunimmaisten väli oli noin puoli metriä. Aika normaalia oppikirjasettiä. Istuin aivan itse varovasti koetaakaksi ja annoin ankkurin asettua pari sekuntia. Tämä noin 0,8 kN koekuorma jakautui pisteiden välille näin:

0,8 kN kuorman jakautuminen solmitulla cordeletella rakennetun ankkurin kolmelle pisteelle (%)

Tässä tapauksessa keskimmäinen piste tuppasi ottamaan 40% ja reunimmaiset siis 30% hujakoilla. Keskihajonta vaihteli 4%-yks. ja 13%-yks. välillä ja oli keskimäärin 10%-yksikköä. Paras tasapainotus oli toiseksi viimeinen, 29-38-33. Voi olla että tässä otannassa on paljon vikaa, ja aion todellakin perehtyä asiaan paremmin. Silti mukana oli myös asiaa auttavia seikkoja, kuten se että kuormituksen suunta oli helppoa arvioida.

Olen ollut kuulevinani kokeneempien ja asiaa myös ymmärtävien suusta koko ajan enemmän sitä väittämää, ettei tasapainottamisella ole oikein mitään tekemistä ankkurin turvallisuuden kanssa. Pitenemisen välttämisellä sitäkin enemmän. Tämä on kiinnostava kaksikko, koska ne ovat osin sama asia, osin ristiriitaisia. Esimerkiksi kiinteä ankkuri kuten y-hang tai solmittu cordelette hoitavat molemmat funktiot samalla tavalla: ne pitää säätää täsmälleen oikean pituiseksi. Sen jälkeen piteneminen on vain "keinahtamista" jäljelle jäävien pisteiden varaan (jolloin tasapainotus tosin väistämättä kärsii). Sliding x tai quad hoitaa tasapainotuksen ainakin muuttuneissa tilanteissa todennäköisesti paremmin, mutta niissä on väistämättä suurempi pidentyminen - eikä tasapainotuskaan välttämättä ole niin hallittua kuin voisi luulla.

Kolme luonnollista varmistuspistettä on tosiaan trädiankkurissa tietynlainen standardi, mutta ne isojen poikien jutut, että joukkoon mahtuisi kuuluisia kuumottavia mikrokiiloja saanee jättää omaan arvoonsa. Se, että kokoaa yhden 7 kN pisteen tasapainottamalla seitsemän 1 kN pistettä on tietenkin juuri niin mahdotonta kuin tasapainottaminen yleensä. On aivan mahdollista, että tuo 10%-yksikön keskihajonta (siis 10% koko kuormasta) pätee myös seitsenhaaraiselle härvelille, mikä siis tarkoittaisi että pisteiden osuudet kuormasta olisivat luokkaa 14+/-10% eli 4%...14% - olisi ihan mahdollista kuvitella jopa kokonaan kuormittumatta jääviä pisteitä. Voisi tosin olla hyvin vaikeaa todella rakentaa seitsemän pisteen ankkuri, joka kuormitettaessa repeää piste kerrallaan kuin paidan napit. Mutta yhtä epätodennäköistä on, että jossain saa sullottua kallioon seitsemän mikrokiilaa muttei yhtään kunnollista piissiä.

Siispä päättelen idean olevan siinä, että ensin otetaan riittävän pienellä todennäköisyydellä pettäviä pisteitä ja sitten tarvittaessa yhdistetään niitä niin, että todennäköisyyksien kertautuminen on riittävän hyvä hypoteesi - siis se, että uuden systeemin pettämisen todennäköisyys on osasysteemien pettämisten todennäköisyyksien tulo. Näin on, kun kullakin pisteellä on riittävä marginaali normaaliin oletettuun käyttökuormaan. Samalla redundanssi tietenkin pienentää murto-osiinsa niitä todennäköisyyksiä, että käyttäjän tekemä karkea virhe on kohtalokas.

Palataan vielä Iratan 6kN x 2,5 -ideaan. Tässä on hyvä syy jakaa varmuuskerroin kahteen osaan, jotka ovat normaalin käytön aiheuttaman kuormituksen vaihteluita ja toisaalta lujuuden vaihteluita varten.

Voisi ikään kuin ajatella, että käyttö lähtee liikkeelle vasemmalta ja vaihtelevilla jakautumilla kurkottelee palkkia oikealle. Lujuus taas lähtee oikealta ja vastaavasti levittäytyy enemmän tai vähemmän normaalijakautuman tyyliin vasemmalle. Sinistä palkkia on mahdollista kasvattaa redundanssilla. Esimerkiksi Iratan mallin mukaan kaksi 10 kN pistettä yhdistettynä vastaavat yhtä 15 kN pistettä.

Sen sijaan vaikkapa 4kN pisteiden yhdistäminen perustuisi jo tasapainottamiseen, sen varmistamiseen, ettei yhdellekään pisteelle tule missään tilanteessa enempää kuin 67% ankkurin kuormasta (pahimmillaan 6 kN). Tämäkin tosin antaisi vain varmuuskertoimen yksi, jonka kompensoimisesta redundanssilla voi keskustella erikseen.

Vielä joku päivä saan paremman otteen tästä aiheesta. Mielessäni vilahtelee normaalijakautumia jotka liittyvät lujuuden lisäksi muihin riskitekijöihin ja aavistelen, etten alkuunkaan ole hoksannut millä kaikilla tavoilla tyhmä tämä kN-asteikolla laskeskeltava turvallisuusnäkökulma on. Ehkäpä palaan asiaan.

Mihin laskeutumislaite piilottaa kaiken energian?

Peruskoulun fysiikasta muistetaan (gravitaatiokentän) potentiaalienergia, jos muistetaan. Kysehän oli siitä, että kun kappaletta nostetaan ylöspäin painovoimakentässä, siihen varastoituu energia E = mgh, jossa m on kappaleen massa, g on painovoimakentän putoamiskiihtyvyys ja h on korkeuden muutos eli kappaleen nousema matka. Tämä energia plus häviöt on hissin tai reppua kantavan porraskävelijän todella kappaleelle luovutettava, ja jos kappale vaikka pudotetaan vastaava matka, sama energia näkyy kappaleen nopeutena, kitkan lämmittämänä ilmana ja niin edelleen.

Tai auton jarrujen lämpenemisenä alamäessä, tai laskeutumislaitteen. Kenties vaikeasti uskottava kohta tässä on se, että koko auton potentiaalienergian muutos todella pitää haihduttaa jarrujen kautta lämpöenergiana taivaan tuuliin, ja sama koskee edelleen laskeutumislaitetta (plus köyttä). Kyse on yllättävän isosta energiamäärästä - kuten kaikki porrastreeniä tehneet uskovat.

Siis. Jos kiipeilijä painaa 80 kg ja laskeutuu 50 m köydenpituuden, johonkin pitää työntää

E = mgh = 80 * 9,81 * 50 J = 39,2 kJ

energiaa. 9,81 m/(s^2) on siis maapallon putoamiskiihtyvyyden normaaliarvo.

Mitä 39 kJ (kilojoulea eli tuhatta joulea) oikein tarkoittaa? Voidaan vaikka tutkia, kuinka paljon sillä saataisiin lämmitettyä erilaisia aineita. Lämpöenergia on siitä mukava (ja hankala) energian muoto, että muut energian muodot lähestulkoon pyytämättä muuttuvat lämmöksi, mutta toiseen suuntaan asia on hankalampi. Esimerkiksi uppokeittimen hyötysuhde on käytännössä 100%. Vanhanaikaisen hehkulampun hyötysuhde on luokkaa 97% - tosin vain jos sillä yritetään tuottaa lämpöä eikä valoa. Se hukkaan menevä osuus (esimerkiksi 97% hehkulampun kohdalla) yleensä on juuri lämpöä.

Lämpöenergia näkyy lämpötilan nousemisena. Lämpöenergia virtaa termodynamiikan toisen pääsäännön mukaan korkeammasta lämpötilasta matalampaa lämpötilaa kohti, kuin alamäkeen, ja ikään kuin pyrkii tasaamaan lämpötilaeron. Mitä suurempi ero, sen jyrkempi mäki ja hanakampi energian siirtyminen. Lämpötila on siis se mitä mitataan lämpömittarilla, lämpö eli lämpöenergia näitä jouleja joista tässä puhutaan.

Veden ominaislämpökapasiteetti on 4,182 kJ/(kgK). Toisin sanoen yhden kilogramman vettä lämmittämiseksi yhdellä asteella (kelviniä tai celsiusta) kuluu reilu 4 kJ. Siispä tällä 50 metrin laskeutumisessa vapautuneella energiamäärällä lämmitettäisiin litraa vettä 9,3 asteella.

Ei kuulosta kovin hurjalta. Mutta entäpä jos oletetaan, että kaikki energia meneekin Petzl Reverso 4:n lämmittämiseen? Reverso painaa 59g ja on alumiininen (ominaislämpökapasiteetti 900 J/(kgK)). Siispä lämpötilan muutokseksi sopisi odottaa 39kJ / (0,059kg * 0,9 kJ/(kgK)) = 734K.

No, oikeasti tämä ei ihan pidä paikkaansa, sillä alumiini sulaa 660 celsiusasteessa, jolloin osa energiasta kuluu ns. faasimuutokseen. Mutta vaikka nyt sovittaisiin että reverso kuumenisi ainoastaan lähelle sulamispistettään, niin jutun ydin varmaan on kaikille selvä. Myöskään se, että oikeasti lämpökuormaa on vastaanottamassa myös sulkurengas, ei muuta mitään oleellista.

Onko vastaus, että lämpöenergia vain haihtuu taivaan tuuliin riittävän nopeasti? Esimerkiksi nopeudella 1m/s sen 50 s aikana, jonka laskeutuminen kestää? Tai jos ajattelee laskeutumista jatkuvana prosessina, 1m/s nopeus tarkoittaisi tehoa

P = vF = vmg = 1m/s * 80kg * 9,81m/(s^2) = 785W,

jossa v on nopeus. Sama arvo saadaan jakamalla energia ajalla: P = 39,2kJ / 50s = 785W.

Otetaanpa vähän perspektiiviä. Tässä hehkutetaan näytönohjainta, jonka prosessorin teho on 260W, eli kolmannes reversosta kuvaillussa tilanteessa. Speksissä kerrotaan myös, että ydin saa kuumeta 89-asteiseksi. Vehje näyttää päältäpäin tältä:

Ilmastoitu aski (nvidia)

Voi helposti päätellä, etteivät nuo puhaltimet ole pelkästään teininörttien ihasteltaviksi. Miksi reverso toimii ilman puhaltimia ja huolellisesti suunniteltuja jäähdytysripoja, vaikka sen teho on kolminkertainen? Miksi näytönohjaimen jäähdyttämiseen ei riitä tietokoneen kotelon yleispuhallin, kun reverson ilmeisesti jäähdyttää pieni kesäinen tuulenvire?

Tuulenvire tai tuollainen ärjy flekti perustuu konvektioon, eli ilmiöön jossa lämpöenergia siirtyy kappaleesta fluidin (nesteen tai kaasun) kyytiin ja virtaa sen mukana pois. Ilmiö on sitä merkittävämpi, mitä enemmän kosketuspinta-alaa kappaleella ja fluidilla on (siksi jäähdytyselementin kymmenet ohuet rivat), lisäksi se riippuu lämpötilaerosta ja fluidikohtaisesta kyvystä siirtää lämoöenergiaa. On esimerkiksi ymmärrettävää, että vesi hoitaa homman ilmaa paremmin. Yksinkertainen mutta toimiva tapa arvioida siirtyvää energiaa on:

Q = U A dT,

missä Q on lämmön siirtymisen teho watteina,  U on fluidikohtainen vakio, A on pinta-ala ja dT on lämpötilaero jäähdytettävän kappaleen ja fluidin välillä.

Oletetaanpa, että reverson pinta-ala on 250 neliösenttiä eli 0,025 m^2. Oletetaan edelleen, että jatkuvassa käytössä 20-asteisessa ympäristössä reverso lämpenisi 80-asteiseksi muttei kuumemmaksi, koska siinä lämpötilassa jäähtyminen tasapainottaisi tilanteen. Edellisestä saadaan:

U = Q/(A dT) = 785W/(0,025m^2 * 60K) = 523 W/m^2K.

Tämä 523 wattia neliömetrikelviniä kohti on siis se fluidikohtainen "jäähdytysteho", jolla saataisiin 785 watin teho siirrettyä ulkopinta-alaltaan 0,025 neliömetrin kappaleesta pois. Tyypillisiä arvoja ilmalle on 10 ... 100 ja vedelle 500 ... 10000.

Toisin sanoen ellen tehnyt tässä mitään karkeita virheitä, ilmavirta ei todellakaan pitäisi reversoa alle 80-asteisena, veden alle upottaminen kenties. Pienen vertailun voi toki tehdä kurkkaamalla kotona vedenkeittimensä tehon. Tässä on yksi malli, jossa 1,2 litraa vettä ei onnistu pitämään 1000-wattista vastusta alle 100-asteisena. Reverson teho ajatuskokeessamme oli kuitenkin niinkin paljon kuin 78% tämän vedenkeittimen tehosta.

No, köysihän on eräänlainen "fluidi". Se koskettaa laskeutumislaitetta ja virtaa sen läpi, joten ehkäpä se kuljettaa lämmön pois? Kitkalämpö siis syntyisi kappaleiden rajapinnassa ja siirtyisi molempiin kappaleisiin materiaalien ominaisuuksien määräämällä tavalla. Aineen kykyä johtaa lämpöenergiaa lävitseen kuvaa lämmönjohtavuus k, jonka yksikkö on W/(mK). Alumiinilla tämä arvo on luokkaa 200  ja nylonilla 0,25. Siirtyvän energian määrä pinta-alayksikköä kohden pisteiden A ja B välillä on fourier'n lain mukaan

Q = k dT/dX,

missä dT on lämpötilaero ja dx etäisyys pisteiden A ja B välillä (jotka toki sijaitsevat samassa köntissä kyseistä materiaalia).

Alumiinissa kahden annetun lämpötilan välillä lämpöenergia siis siirtyy 800 kertaa niin tehokkaasti kuin nylonissa. Se, että köydessä kaiken lisäksi on kolmasosa ilmaa, ei paranna tilannetta nylonin hyväksi.

Mistäkö muuten repäisin tämän suhteen? Nylonin tiheys on noin 1,15 kg/l. Beal Access 11mm painaa 73g per metri. Metrin pätkän halkaisijaltaan 11-millistä köyttä tilavuuden voi laskea olevan 0,095 litraa, joten jos se olisi umpinylonia, sen kuuluisi painaa 0,109 kg. 73g/109g = 67%, lähestulkoon liian tarkasti kaksi kolmasosaa.

Takaisin asiaan. Tehdään pieni ajatuskoe. Oletetaan, että ympäristön lämpötila on 20 astetta ja laskeutumislaitteessa kitka synnyttää alumiinin ja nylonin rajapinnassa 80 asteen lämpötilan. Köyden (tätä pientä kosketuspintaa lukuun ottamatta) voi ajatella koko ajan pysyvän 20-asteisena, koska kitkan lämmittämä köysi poistuu välittömästi paikalta ja tilalle tulee uutta, ympäristön lämpöistä köyttä - tästä itse asiassa on kyse ylempänä esitetyssä konvektiossa. Laskeutumislaite taas lämpenee niin, että jonkin matkan päässä kontaktipinnasta lämpötila on tasainen 50 astetta. Tällöin nylonissa lämpöenergia virtaa 80 asteen lämmöstä kohti 20 asteen aluetta, kun taas alumiinissa 80 asteesta 50 asteeseen. Ero on siis nylonissa 60 astetta ja alumiinissa 30 astetta. Ja juuri tämä lämpötilaero saa lämpöenergian virtaamaan, se on kuin alamäki mitä painovoimaan tulee.

Jos oletetaan muut tekijät molemmille kappaleille samoiksi, kaksinkertaisen lämpötilaeron takia nylon siirtääkin lämpöenergiaa jo 1/400 teholla alumiiniin nähden. Siis ylemmän esimerkin 785W tehosta köyteen menisi 2W ja laskeutumislaitteeseen 733W.

Mutta köysihän syöttää koko ajan uutta 20-asteista nylonia imemään lämpöä. Silloinhan voidaan ajatella, että nylonissa 80-asteisen kitkapinnan ja lähimmän 20-asteisen kohdan etäisyys (alla olevassa kuvassa t) on hyvin lyhyt, nollaa lähestyvä. Nollan paksuisesta kerroksesta nylonia lämpö toki siirtyy äärettömällä teholla, jos vain lämpötilaero on olemassa.

Ja tosiaan, voidaan laskea t jolla lämmönjohtumisen teho olisi 785W. Fourier kertoo meille, että yhden neliösentin alalla tällainen paksuus olisi kaksi mikrometriä. Jos 20 asteen lämpötilaan olisi pidempi "liukumäki", ei näin suuri teho jaksaisi kulkea. Lämpöä ei selvästikään kulje yhtään pidemmäs kuin t:n matkalle, koska muussa tapauksessa lämpötila nousisi ja 20 asteen raja työntyisi eteenpäin - eli t kasvaisi. On siis oletettava, että kaikki köyteen siirtynyt lämpö majailee tässä kahden mikrometrin paksuisessa kaistaleessa.

Voisiko homma silti toimia? Tunnen itseni tyhmäksi, kun en osaa tuottaa kivoja differentiaaliyhtälöitä jotka kuvaisivat ilmiön kauniisti. Siispä rumempi tie: Näitä yhden neliösenttimetrin kontaktialoja mahtuu metrin matkalle köyttä koko lailla sata kappaletta. Jokaisen matkalla olisi siis siirrettävä 785J/100 = 7,85J. Jos nyt oletetaan, että tilavuus on umpinaista nylonia 67-prosenttisen köyden sijasta, kunkin kontaktialan alle mahtuvan kaistaleen tilavuus olisi 2um*1m*10mm = 0,2 mikrolitraa ja massa 23 mikrogrammaa. Nylonin lämpökapasiteetti on 1600 J/kgK, joten jos tällaiseen kappaleeseen työnnettäisiin 7,85J lämpö, lämpötilan muutos olisi 21300 astetta.

Tässä siis oletettiin, että koko laskeutumisessa vapautuva lämpö menisi pinnan läpi köyteen. Kaikki yhtälöt ovat mukavasti lineaarisia, joten tuloksista on helppoa johtaa ajatuskokeita. Esimerkiksi jos vain puolet lämmöstä menisi köyteen, riittäisi neljän mikrometrin lämmönsiirtokerros, jonka tuplatilavuus lämpenisi puolikkaalla energialla vain neljänneksen edellisestä: 5300 astetta. Kahdeskymmenesosa lämmöstä: 0,01 mm paksu kaistale, 12 milligrammaa nylonia ja 0,39J lämpöä jemmattavaksi: 53 astetta.

Viimeinen siis kuulostaa jollain lailla järkevältä. Laskentatapa on kuitenkin niin karkea, että vaikkei se sisältäisikään mitään katastrofaalisen typerää joka tekee kaikista tuloksista roskaa, mitään näin tarkkaa sillä ei kannata yrittää päätellä. Siitä olen kuitenkin vakuuttunut, ettei nylonköyden pinnan läpi saa johtumaan kymmentäkään prosenttia laskeutumisessa vapautuvasta lämmöstä.

Mihin lämpö sitten menee? Luulen että oleellisimpi kysymys on, missä se syntyy. Nylonin ominaislämpökapasiteetti on melko hyvä, 1600 J/kgK. Se on esimerkiksi alumiiniin verrattuna yli kolminkertainen (tosin nylonin tiheyskin on alle puolet alumiinin tiheydestä). Joka tapauksessa lämmön säilöminen köyteen ei ole ongelma. 785J/m lämmittää 76g/m köyttä noin kuudella asteella, joka kuulostaa vallan tolkulliselta.

Hankaluuksia tulee, jos on selitettävä lämmön liikkuminen köydessä. Siispä mikäpä olisi mukavampi kuin teoria, jossa mekaaninen työ muuttuu lämmöksi koko köyden tilavuudessa. Jotain tällaista tapahtuu, jos köysipyörässä tai laskeutumislaitteessa mutkalle pakotetussa köydessä syntyvä kitka perustuukin pitkälti köyden sykliseen venymiseen (ulkokehällä venyy, sisäkehällä painuu kasaan) ja samalla hystereesiin katoavaan energiaan.

Asiaa lienee tutkittava lisää.