Talja-analyysia 2: taljat vertailussa

Aiemmin yritin kvantifioida yksittäisten köysipyörien merkitystä koko taljan hyötysuhteen eli efektiivisen voimakertoimen kannalta. Mutta mitä jos unohtaa yksittäiset pyörät ja vertaa erilaisia taljoja sillä oletuksella, että kaikki pyörät ovat identtisiä?

Otetaan esimerkiksi 9:1 (z on z). Sen voima-analyysin tulos on

1+
P1+P3+
P1P2+P1P3+P3P4+
P1P2P3+P1P3P4+
P1P2P3P4

eikä nyt ole mitään merkitystä sillä, mikä hyötysuhteista P1...P4 on minkäkin pyörän, koska seuraavaksi oletetaan ne kaikki samoiksi P. Silloin jäljelle jää polynomi:

1 + 2P + 3P^2 + 2P^3 + P^4

Jonka voi näppärästi ilmaista myös termien kertoimilla asteluvuittain:

0. 1
1. 2
2. 3
3. 2
4. 1

Kaikki matematiikan tunnilla hereillä olleet muistavat polynomifunktion kuvaajan, ainakin toisen asteen paraabelin mallisen. Mitä kuvaaja tässä tapauksessa esittää? Taljan efektiivistä voimakerrointa kun sen pyörien hyötysuhde vaihtelee. Hyötysuhteen todellisen maailman arvot ovat välillä 0...1, joten sen enempää ei kannata käyrääkään piirrellä. Pelkät sulkurenkaat ovat siis jossain puolen tienoilla (uskon että alapuolella), ja oikein hyvät kuulalaakeroidut pyörät 0,9 luokkaa.

9:1 ja 11:1 -taljojen laskennalliset voimakertoimet köysipyörien hyötysuhteilla 0-1

Kuvaajassa on mukana myös z on z -tyyppinen 11:1, jonka polynomikertoimet ovat

0. 1, 1. 2, 2. 4, 3. 3, 4. 1

Eli toisen ja kolmannen asteen kertoimet ovat yhden pykälän isompia. Kuvaajaa katsoessa pitää varoa unohtamasta, että taljoilla on eri ideaaliset taljasuhteet - joissa suhteissa köyttä on joka tapauksessa niistä kiskottava. Lukeminen kannattaa aloittaa oikealta, ykkösen kohdalta, joka tietyllä tavalla näyttää taljan odotusarvon. Se, mitä tapahtuu todellisen elämän hyötysuhteilla eli siirryttäessä kohti kuvaajan keskiosaa, osoittaa kuinka hyvin tai huonosti 11:1 perustelee itsensä verrattuna 9:1:een. Esimerkiksi kodassa 0,8 arvot ovat 7,1:1 ja 5,9:1, eli oikeastaan ero on vajonnut puoleen - ja edelleen on vedettävä täydet 11 metriä köyttä kuorman nostamiseksi yhden metrin matkan.

On kuitenkin kiinnostavampiakin käyräkaksikoita. Esimerkiksi yksinkertaisen 7:1:n (jota harva luuleekaan hyväksi taljaksi) ja tämän alaspäin vedettävän kompleksin 7:1:n:

Mielenkiintoinen 7:1

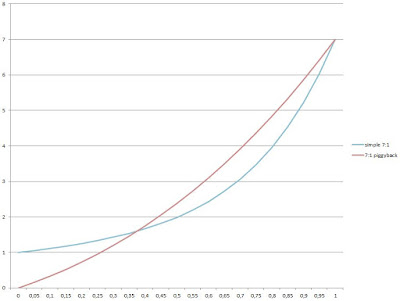Yksinkertainen 7:1 ja kompleksi alaspäin vedettävä 7:1

Siitä huolimatta että kompleksin systeemin polynomista puuttuu nollas aste eli ykkönen ja siis käyrä alkaa nollasta (koska taljaa vedetään alaspäin), se ohittaa simppelin ylöspäin vedettävän systeemin alle 0,4:n kohdalla, eli kaikki tosielämän käyttökelpoiset pyörät tai niiden korvikkeet ovat sen vahvemmalla alueella. Suurimmillaan ero on kohdassa 0,75, jossa simppelin systeemin efektiivinen kerroin on 3,5:1 ja kompleksin 4,4:1. Tämä on hauskasti aika hyvä arvaus pienen, railo- tms. pelastustilanteissa käytettävän pyörän hyötysuhteeksi. Toivottavasti kovin monelle ei tullut yllätyksenä: kierrosten lisääminen simppeliin taljaan ei auta mitään, on tehtävä jotain juonikkaampaa.

Kannattaako vetää z-rigiä 2:1:llä vai toisin päin? Verrataan kahta 6:1- ja yhtä 5:1-taljaa. Toinen 6:1 on z-rig joka vetää 2:1-systeemiä ja toinen toisin päin. 5:1 on suosittu z-rig-kehitelmä, jossa yhteen väliin on lisätty 2:1. Olen nähnyt sitä kutsuttavan "5:1 crevasseksi".

Edelliset kolme taljaa vertailussa

Paitsi että kannattaa rakentaa z-rig vetämään 2:1-systeemiä, niin kannattaa yhtään kehnommilla pyörillä jopa mieluummin rakentaa 5:1. Jos on yhtään kiinnostunut energiasta, joka kuorman nostamiseen kuluu, 5:1 on helposti taloudellisempi. Energia eli työ on yhtä kuin voima kertaa matka, ja tässä tapauksessa kiinnostaa tietysti vedettävän köyden kulkema matka ja vetämiseen tarvittava voima. Ja jos kuormaa nostetaan sama matka, 5:1-taljalla köyttä on vedettävä 5/6 6:1-taljan määrästä.

Yleisesti ottaen käyrät siis yhdistävät pisteen 0,1 (tai 0,0) pisteeseen 1,N, missä N on taljan ideaali voimakerroin. Käyrän "roikkuminen" osoittaa erot ideaalisti samanlaisten taljojen välillä ja on siis huono ominaisuus. Ideaali olisi suora, lineaarisen polynomin kuvaaja, eli sellaisen jossa on vain nollatta ja ensimmäistä astetta. Sellainen on 2:1-taljalla, jonka polynomi on 1+P. En nyt piirrä kuvia enkä kuvaajia.

Mitä korkeampaa astetta olevia termejä polynomissa on ja mitä suurempia niiden kertoimet ovat, sen enemmän sen kuvaaja roikkuu välillä 0..1. Ja mitä enemmän kuvaaja roikkuu, sitä tärkeämpää on käyttää köysipyöriä, joiden hyötysuhde on mahdollisimman iso. Oikein jyrkästi nouseva kuvaaja vaan saattaa roikkua kohtuuttoman paljon jo superhyvän köysipyörän arvoilla. Esimerkiksi simppeli 7:1 antaa P:n arvolla 0,9 voimakertoimen 5,2:1.

Otetaanpa vielä yksi kuvaaja. Siitä ei tarvitsekaan saada yksityiskohtaisesti selvää, pääasia että yleinen hahmo erottuu.

Nippu taljoja

Kuvaajan opetus on, että jos rakentaa taljasysteemin käyttämällä sulkurenkaita pyörien sijasta (oletetaan optimistisesti hyötysuhteeksi 0,5), sen efektiivinen voimakerroin on alle neljä, oli se sitten miten monimutkainen vain. 3,5:1:n tapauksesta vain on kiskottava köyttä 3,7-kertainen määrä 1,5:1:een verrattuna ja resetoitava päntiönään. Siispä kannattaa mieluummin ottaa kaksi kättä lisää kiskomaan kuin lisätä systeemiin kaksi sulkurengasta.