Talja-analyysia 3: osien nopeudet ja resetointipersous

Taitavat taljalaskut olla yhdysvalloissa high schoolien ja collegejen peruskauraa. Googlella löytyy paljon osumia, mutta ne eivät juurikaan liity köysityöskentelyyn tai muuhun käytännölliseen. Lisäksi ne keskittyvät epäkäytännöllisten - mitä hässäkkäisempien sitä parempi - systeemien ideaalin voimakertoimen selvittämiseen. Voi olla etten tiedä oikeita hakutermejä, mutta en tosiaan ole löytänyt kunnollista käsittelyä edes voima-analyysille, jota äskettäin vähän harrastelin.

Tällaista löytyy senkin edestä (www.physicsforums.com). En tiedä trollaako vastaaja, mutta ainakaan itse en ole samaa mieltä yhdestäkään vastauksesta. No, itsekin kirjoittelen kaikkien nähtäville omia käsityksiäni asioista, mutta en sentään erityisesti tarjoa vastauksia kellekään. Oli miten oli, taso on tätä. Vaikka useimmin ideaalit taljakertoimet menisivätkin oikein, hyötysuhtesiin saakka ei edes yritetä mennä. Mutta sikäli kiinnostavia nuo lukion saivartelut, että normaalisti itse käyttämälläni menetelmällä ne kaikki eivät ratkea.

Pöhkö koulutehtävä

Normaalisti teen vetopäästä lähtien voima-analyysin, mutta oletan hyötysuhteet ykkösiksi jolloin saan suoraan kussakin komponentissa olevan ideaalisen voiman. Mutta kappas. Tässäpä talja haarautuukin nurinkurisesti normaaliin nähden. Ei voi tietää, kuinka voima F jakautuu kahdelle pienelle pyörälle. Kyllä, tämän systeemin toki voisi ratkaista takaperin, koska se ei todellakaan missään kohdassa haaraudu normaalilla tavalla. Mutta jos haarautuisi, jos vaikka ison pyörän 2:1 tilalla olisi z-rig tai jotain monimutkaisempaa, silloin voima-analyysi tyssäisi molemmista suunnista ja jouduttaisiin paloittelemaan ongelma tilanteen mukaan.

Voiman jakautumista haarassa ei ole triviaalia selvittää, mutta köyden liikkuminen on. Jos nimittäin sovitaan, että nuolen kohdalta vedetään nopeudella s (suhteessa ankkuriin), voidaan olla varmoja että molemmat köyden haarat liikkuvat tällä nopeudella. Silloin riittää, että edes toinen pyöristä on kiinnitetty suoraan ankkuriin (aina ei välttämättä ole, mutta se on toinen murhe). Sovitaan, että liikkeen positiivinen suunta on kuorman nostosuuntaan. Köyttä vedetään siis nopeudella -s. On helppoa ymmärtää, että ankkurissa kiinni oleva eli paikallaan oleva pyörä vain kääntää liikkeen suunnan, joten alempi pieni pyörä liikkuu nopeudella s.

Mitä tapahtuu sille köyden haaralle, joka menee alempaan, ylöspäin liikkuvaan pyörään? Kuvittele pyörä 2:1-systeemin osana. vaikka köysi pyörän oikealla puolella pysyisi paikallaan, jos pyörä liikkuu nopeudella s, toisella puolella köysi liikkuu nopeudella 2s. Kun siihen lisätään köyden liike -s suuntaa vaihtaneena eli s, saadaan 3s. Ja yleisessä tapauksessa S2 = 2*SP - S1, missä S2 on köyden liike pyörän jälkeen, SP pyörän liike ja S1 köyden liike ennen pyörää. Kaikki nopeudet ovat suhteessa ankkuriin.

Ei varmaan tarvita neljättä kuvaa selvittämään loppua. 2:1-talja puolittaa nopeuden, joten lopputulos on 1,5s. Kun tämä hirvitys kuvitellaan ideaaliksi, voimakerroin on siis 1:1,5. Olisiko nopeusanalyysista muuta iloa kuin joidenkin voima-analyysilla ratkeamattomien tilanteiden selvittäminen?

No kyllä, sillä voi tutkia taljan komponenttien keskinäisiä nopeuksia ja ennustaa niiden törmäämishetkiä. Toisin sanoen sitä, kuinka paljon köyttä voidaan vetää ennen kuin on resetoitava. Pitäisi keksiä hyvä suomenkielinen nimi taljan alttiudelle ajautua resetointia vaativaan tilanteeseen (tosin "resetoida" ei ole suomea sekään). Tässä erittäin hyvässä Youtube-videossa asiaa sivutaan ja käytetään termiä collapse rate. Videolla muuten päätellään pyörien nopeus ihan otsaluulla katsomalla, mutta jopa joissain käytännöllisissä taljoissa se ei ole niin helppoa - akateemisesta hifistelystä puhumattakaan. Puhun toistaiseksi collapse ratesta (CR) mieluummin kuin puristan väkisin harkitsemattoman suomenkielisen sanan. Kuten vaikka "resetoinnille persous" eli RP.

CR tarkoittaa videolla sitä kerrointa, jolla resetointia vaativaan tilaan etenevän traktorin nopeus on suurempi kuin kuorman nopeus. Siispä nostaakseen kuormaa taljan pituuden verran on ko. traktoria resetoitava CR kertaa (hieman idealisoituna). Oikeassa elämässä taljan pituus on epämääräinen käsite ja resetointitarve riippuu myös "traktorien" pituuksista. Lainaan David Fasulon kirjaa paremman termin puutteessa viittaamaan tarraimen ja pyörän yhdistelmään, ja tässä tekstissä jätän tästä lähin traktorin ympäriltä lainausmerkit pois. Oikeassa elämässä ei tietenkään voi nostaa kuormaa taljan mittaa resetoimatta välillä myös siten, että taljan pituus palaa ennalleen.

Taljan ja "traktorien" pituudet (kuvittele punaisen levyn tilalle tarrain)

Mielestäni taljan pituus teoreettisessa mielessä määräytyy kauimmaisten köysipyörien akselien mukaan. Käytännössä ketjua voi jatkaa kattamaan sulkurenkaat ja ties mitä, jos niin haluaa. Traktorien pituudet jättäisin lähtökohtaisesti huomioimatta. Matemaattisesti tämän voisi linjata niin, että käsitellään taljaa, jonka pituus lähenee ääretöntä - silloin äärellisen mittaiset traktorit ja muu oikeassa elämässä hankala voidaan näppärästi sivuuttaa. Aina kun tällaisia sivuutuksia tehdään, täytyy kuitenkin muistaa palauttaa ikävät asiat mieleen ja ottaa ne huomioon kun sen aika on.

Tehdään kokeeksi nopeusanalyysi tuolle 11:1-taljalle ja verrokiksi vastaavalle 9:1:lle (z-rig on z-rig). Kuvissa on esitetty kaavamaisesti osien liikesuunnat ja suhteelliset nopeudet sekä kohta, jossa tapahtuu törmäys ellei resetoida ajoissa.

11:1, nopeusanalyysi ja kohta, jossa traktorit törmäävät

9:1, nopeusanalyysi ja kohta, jossa traktori törmää kääntöpyörään

Kuva on sikäli hieman epäreilu 11:1-systeemiä kohtaan, että vaikka luvattiin olettaa taljat äärettömän pitkiksi, kaavioiden taljat ovat sen sijaan hyvin lyhyitä suhteessa traktorien pituuksiin. Jos traktorien pituudet unohdetaan, 11:1:llä voi nostaa taakkaa 3/4 taljan pituudesta siinä missä 9:1:llä päästään koko taljan pituus. Todellisuudessa toisen traktorin ilmestyminen kuvioihin - lyhentämään matkaa jonka traktorit pääsevät liikkumaan - voi olla merkittävämpi tekijä resetointien tiheyden suhteen. Täytyypä ehkä joskus tehdä jotain käytännöllisempiä kokeita, siis oikein mittanauhan kanssa.

9:1:n CR on helppo tapaus, se on tietenkin kolme. Mutta 11:1 kohdalla on ilmeisesti laskettava törmäävien traktoreiden lähestymisnopeus, neljä. Se merkitsee, että 9:1 on resetoitava kolme kertaa ja 11:1 neljä kertaa taljan mittaisen kuorman nostamisen aikana. Veikkaan, että vaikkapa tosi kireän köysiradan pingottamiseen tämä olisi ihan ok, mutta ei mihinkään taakkojen nosteluun.

Talja-analyysia 2: taljat vertailussa

Aiemmin yritin kvantifioida yksittäisten köysipyörien merkitystä koko taljan hyötysuhteen eli efektiivisen voimakertoimen kannalta. Mutta mitä jos unohtaa yksittäiset pyörät ja vertaa erilaisia taljoja sillä oletuksella, että kaikki pyörät ovat identtisiä?

Otetaan esimerkiksi 9:1 (z on z). Sen voima-analyysin tulos on

1+
P1+P3+
P1P2+P1P3+P3P4+
P1P2P3+P1P3P4+
P1P2P3P4

eikä nyt ole mitään merkitystä sillä, mikä hyötysuhteista P1...P4 on minkäkin pyörän, koska seuraavaksi oletetaan ne kaikki samoiksi P. Silloin jäljelle jää polynomi:

1 + 2P + 3P^2 + 2P^3 + P^4

Jonka voi näppärästi ilmaista myös termien kertoimilla asteluvuittain:

0. 1
1. 2
2. 3
3. 2
4. 1

Kaikki matematiikan tunnilla hereillä olleet muistavat polynomifunktion kuvaajan, ainakin toisen asteen paraabelin mallisen. Mitä kuvaaja tässä tapauksessa esittää? Taljan efektiivistä voimakerrointa kun sen pyörien hyötysuhde vaihtelee. Hyötysuhteen todellisen maailman arvot ovat välillä 0...1, joten sen enempää ei kannata käyrääkään piirrellä. Pelkät sulkurenkaat ovat siis jossain puolen tienoilla (uskon että alapuolella), ja oikein hyvät kuulalaakeroidut pyörät 0,9 luokkaa.

9:1 ja 11:1 -taljojen laskennalliset voimakertoimet köysipyörien hyötysuhteilla 0-1

Kuvaajassa on mukana myös z on z -tyyppinen 11:1, jonka polynomikertoimet ovat

0. 1, 1. 2, 2. 4, 3. 3, 4. 1

Eli toisen ja kolmannen asteen kertoimet ovat yhden pykälän isompia. Kuvaajaa katsoessa pitää varoa unohtamasta, että taljoilla on eri ideaaliset taljasuhteet - joissa suhteissa köyttä on joka tapauksessa niistä kiskottava. Lukeminen kannattaa aloittaa oikealta, ykkösen kohdalta, joka tietyllä tavalla näyttää taljan odotusarvon. Se, mitä tapahtuu todellisen elämän hyötysuhteilla eli siirryttäessä kohti kuvaajan keskiosaa, osoittaa kuinka hyvin tai huonosti 11:1 perustelee itsensä verrattuna 9:1:een. Esimerkiksi kodassa 0,8 arvot ovat 7,1:1 ja 5,9:1, eli oikeastaan ero on vajonnut puoleen - ja edelleen on vedettävä täydet 11 metriä köyttä kuorman nostamiseksi yhden metrin matkan.

On kuitenkin kiinnostavampiakin käyräkaksikoita. Esimerkiksi yksinkertaisen 7:1:n (jota harva luuleekaan hyväksi taljaksi) ja tämän alaspäin vedettävän kompleksin 7:1:n:

Mielenkiintoinen 7:1

Yksinkertainen 7:1 ja kompleksi alaspäin vedettävä 7:1

Siitä huolimatta että kompleksin systeemin polynomista puuttuu nollas aste eli ykkönen ja siis käyrä alkaa nollasta (koska taljaa vedetään alaspäin), se ohittaa simppelin ylöspäin vedettävän systeemin alle 0,4:n kohdalla, eli kaikki tosielämän käyttökelpoiset pyörät tai niiden korvikkeet ovat sen vahvemmalla alueella. Suurimmillaan ero on kohdassa 0,75, jossa simppelin systeemin efektiivinen kerroin on 3,5:1 ja kompleksin 4,4:1. Tämä on hauskasti aika hyvä arvaus pienen, railo- tms. pelastustilanteissa käytettävän pyörän hyötysuhteeksi. Toivottavasti kovin monelle ei tullut yllätyksenä: kierrosten lisääminen simppeliin taljaan ei auta mitään, on tehtävä jotain juonikkaampaa.

Kannattaako vetää z-rigiä 2:1:llä vai toisin päin? Verrataan kahta 6:1- ja yhtä 5:1-taljaa. Toinen 6:1 on z-rig joka vetää 2:1-systeemiä ja toinen toisin päin. 5:1 on suosittu z-rig-kehitelmä, jossa yhteen väliin on lisätty 2:1. Olen nähnyt sitä kutsuttavan "5:1 crevasseksi".

Edelliset kolme taljaa vertailussa

Paitsi että kannattaa rakentaa z-rig vetämään 2:1-systeemiä, niin kannattaa yhtään kehnommilla pyörillä jopa mieluummin rakentaa 5:1. Jos on yhtään kiinnostunut energiasta, joka kuorman nostamiseen kuluu, 5:1 on helposti taloudellisempi. Energia eli työ on yhtä kuin voima kertaa matka, ja tässä tapauksessa kiinnostaa tietysti vedettävän köyden kulkema matka ja vetämiseen tarvittava voima. Ja jos kuormaa nostetaan sama matka, 5:1-taljalla köyttä on vedettävä 5/6 6:1-taljan määrästä.

Yleisesti ottaen käyrät siis yhdistävät pisteen 0,1 (tai 0,0) pisteeseen 1,N, missä N on taljan ideaali voimakerroin. Käyrän "roikkuminen" osoittaa erot ideaalisti samanlaisten taljojen välillä ja on siis huono ominaisuus. Ideaali olisi suora, lineaarisen polynomin kuvaaja, eli sellaisen jossa on vain nollatta ja ensimmäistä astetta. Sellainen on 2:1-taljalla, jonka polynomi on 1+P. En nyt piirrä kuvia enkä kuvaajia.

Mitä korkeampaa astetta olevia termejä polynomissa on ja mitä suurempia niiden kertoimet ovat, sen enemmän sen kuvaaja roikkuu välillä 0..1. Ja mitä enemmän kuvaaja roikkuu, sitä tärkeämpää on käyttää köysipyöriä, joiden hyötysuhde on mahdollisimman iso. Oikein jyrkästi nouseva kuvaaja vaan saattaa roikkua kohtuuttoman paljon jo superhyvän köysipyörän arvoilla. Esimerkiksi simppeli 7:1 antaa P:n arvolla 0,9 voimakertoimen 5,2:1.

Otetaanpa vielä yksi kuvaaja. Siitä ei tarvitsekaan saada yksityiskohtaisesti selvää, pääasia että yleinen hahmo erottuu.

Nippu taljoja

Kuvaajan opetus on, että jos rakentaa taljasysteemin käyttämällä sulkurenkaita pyörien sijasta (oletetaan optimistisesti hyötysuhteeksi 0,5), sen efektiivinen voimakerroin on alle neljä, oli se sitten miten monimutkainen vain. 3,5:1:n tapauksesta vain on kiskottava köyttä 3,7-kertainen määrä 1,5:1:een verrattuna ja resetoitava päntiönään. Siispä kannattaa mieluummin ottaa kaksi kättä lisää kiskomaan kuin lisätä systeemiin kaksi sulkurengasta.

Talja-analyysia

Keksin (ihan liian pitkään mietittyäni) edes jonkinlaisen tavan kvantifioida yksittäisen köysipyörän hyötysuhteen merkitystä taljan kokonaishyötysuhteen kannalta. Sehän on melko yleisesti tunnettu nyrkkisääntö, että lähelle nyrkkiä (hehe) laitetaan paras pyörä. Siis se pyörä, jonka läpi köysi ensimmäisenä menee taljasysteemin sisään, merkitsee eniten. Asia on helppoa selittää niin, että tämän pyörän kitka haukkaa osansa kaikesta siitä energiasta, jota taljaan vetämällä syötetään. Se on kuin valtion verotus, jonka päälle muut pyörät vielä asettavat kuntaveronsa.

Mutta entä ne muut pyörät? Missä järjestyksessä pitäisi jakaa liukkaat pyörät, ja kuinka isoja eroja pyörien merkityksessä on? Tutkitaan 5:1-systeemiä, joka on esitelty mm. David Fasulon kirjassa Self-Rescue (s. 130).

Analysoitava 5:1

Tehdään pyörälle voima-analyysi, jonka periaatteet muuten myöskin ohimennen esitellään samassa kirjassa. Kyse ei ole mistään kovin ihmeellisestä tempusta. Siinä vain oletetaan, että kun köysipyörän toiselta puolelta vedetään köydestä voimalla F, toisella puolella pyörää olevassa köydessä on voima F * P1, missä P1 on köysipyörän hyötysuhde (ja köyden on toki oltava ankkuroitu johonkin niin, että se vain kiristyy muttei liiku). Hyötysuhdehan on kerroin jonka arvo on 0-1. Muistutetaan tässä välissä, että 100% on tasan 1, ja on makuasia ilmoittaako hyötysuhteeksi vaikkapa 80% vai 0,8. Tässä pohdinnassa puhutaan enemmän jälkimmäisellä tavalla.

Lähdetään liikkeelle taljan vetopäästä, oletetaan että siinä on voima F. Sitten käydään talja läpi kohti kuorman päätä, kertoen kertynyt voima aina kunkin pyörän jälkeen pyörän hyötysuhteella ja tarrainten tai muiden y-haarojen kohdalla summataan haarojen voimat. Merkitään hyötysuhteita P1, P2 jne. Kerroin F voidaan jättää pois, jolloin siis ei lasketa läpi menevää voimaa vaan kerrointa, jolla voima kerrottaisiin.

Kertoimen yhteisvaikutuksena saadaan efektiivinen taljakerroin, eli hyötysuhteella kerrottu ideaalinen kerroin. Z-rigin efektiivinen kerroin voisi olla vaikka 0,75*3:1 eli 2,25:1.

Talja analysoituna

En ollut oikein koskaan vaivautunut tekemään tätä, etenkään niin että pitää hyötysuhteet muuttujina eikä laske suoraan joillan oletetuilla arvoilla. Olisi kannattanut jo ajat sitten, koska äkkiä huomasin erään mielenkiintoisen seikan. Lausekkeeseen tulee aina yhtä monta termiä kuin mikä taljan ideaalinen kerroin on, esimerkiksi tässä tapauksessa viisi: 1, P1, P2, P1*P2, P1*P3. Ja sehän käy järkeen! Koska termit ovat joko 1, yksittäisen pyörän hyötysuhde tai useamman pyörän hyötysuhteiden tulo, niiden arvot väistämättä ovat välillä 0-1. Niinpä maksimiarvo on viisi, aivan kuten pitääkin.

Ykkönen ilmestyy silloin, kun taljaa vedetään samaan suuntaan kuorman liikkeen kanssa, ja se ilmentää sitä, että köyden voima (1*F) vetää kuormaa sellaisenaan kulkematta yhdenkään pyörän läpi. Pyörättömän köyden hyötysuhde on toki 1. Tämä on yksi viidestä (tässä tapauksessa) reitistä, jota pitkin voima siirtyy taljan läpi. Muut reitit kulkevat yhden tai kahden pyörän kautta. Yhden pyörän kautta kulkeva reitti tuottaa termit P1 ja P2, kun taas esimerkiksi P1*P3 kulkee pyörien P1 ja P3 kautta.

Huomautetaan tässä välissä, että enää en lainaa Fasulon kirjaa tai muutakaan viisaampien opettamaa, vaan vedän hatusta. Reittianalyysi käy järkeeni, mutta se nyt vielä ei paljon merkitse. Siispä kuten aina, epäile netistä lukemaasi.

Reittien selvittämistä auttaa, jos kuvittelee kaikki muut paitsi termissä esiintyyvät pyörät jumittuneiksi. Esimerkiksi P2: jos P1 ja P3 lukitaan, lopputuloksena on 2:1-talja:

P2, 2:1

P1P3 taas ilmentää z-rigiä:

P1P3, 3:1

Loput kolme voiman reittiä tai "osataljaa":

Termejä 1, P1 ja P1P2 vastaavat voiman reitit

Sitä en vielä ole itselleni selvittänyt, miksi 5:1 tässä tapauksessa koostuu komponenteista 1:1, 2:1, 2:1, 3:1 ja 4:1. Näistä toistaiseksi selittämättömistä luvuista huolimatta on melko selvää, että laskennallinen efektiivinen hyötysuhde todella vaihtelee välillä 0-5, ja että jokainen näistä viidestä termistä vaikuttaa siihen tasan yhden viidesosan verran kukin.

Mutta mitkä ovat eri pyörien osuudet? Jos lasketaan kuinka monessa termissä kukin esiintyy, saadaan

• P1: 3 kertaa
• P2: 2 kertaa
• P3: 1 kerran

Ainakin tästä voidaan päätellä, että pyörä yksi pääsee sotkemaan kolmea voiman viidestä reitistä. Ja todella, ykköspyörähän on se nyrkkisäännönkin mukaan kriittinen tapaus. Termit 1 ja P2 pysyvät arvoiltaan samoina, vaikka P1 olisi nolla eli pyörä yksi aivan jumiin ruostunut. Joten ideaalisillakin pyörillä 2 ja 3 päästäisiin korkeintaan taljasuhteeseen 2:1.

Jos taas unohdetaan ideaalisuudet ja oletetaan kahden muun pyörän hyötysuhteeksi 0,8, saadaan seuraavan kuvaajan mukaiset teholliset taljasuhteet, kun tutkittava pyörä saa hyötysuhteet 0-1 (edellä lasketun analyysin mukaan).

Taljan efektiivinen kerroin, jos kunkin pyörän hyötysuhde vaihtelee välillä 0-1 toisten kahden pyörän hyötysuhteen ollessa 0,8

Kulmakertoimet ovat:

• P1: 2,6
• P2: 1,8
• P3: 0,8

Jotka todellakin ovat suoraan verrannollisia esiintymistiheyksiin (karkeasti ottaen kertoimella 0,9). En nyt mene formaalimpaan todistelemiseen, koska pidän simuloidusta empiriasta. Kuvaajat ovat kivoja.

Mutta tämä koskee vain tätä taljaa ja 0,8:n hyötysuhteella toimivia muita pyöriä. Mitä voitaisiin sanoa yleisesti ottaen pyörän vaikutuksesta kokonaisuuteen? 

Merkitäänpä niitä termejä, joissa esiintyy P1, tunnuksilla P1-1, P1-2, P1-3 jne. ja muita Px-1, Px-2 jne. Jos P1:n hyötysuhde nyt putoaisikin puoleen, kokonaishyötysuhde olisi

(P1-1 + P1-2 + P1-3 + ... + P1N) * 0,5 + (Px-1 + Px-2 + ... + PxM)

Tämän taljan ideaalinen voimakerroin on siis N+M (termien määrä yhteensä), ja P1 on mukana N:ssä niistä. Keskimäärin, oikein tilastollisesti ajateltuna, voidaan ehkä olettaa että molempien joukkojen termit ovat yhtä suuria - siis keskimäärin - sovitaan vaikka, että keskiarvo on P. Silloin kokonaishyötysuhde olisi

0,5NP + MP = P(0,5N +M)

Eli kerroin alkuperäiseen nähden olisi

(0,5N+M)/N+M.

Esimerkiksi aiemmin tutkitun 5:1-systeemin tapauksessa (0,5*3) + 2 / (3+2) = 0,7. Varmaan ihan hyvä arvaus, mutta tässä vaiheessa ei auta hyväksyä noin karkeita oletuksia, kun kuitenkin on aloitettu analysoimalla taljasysteemi aika hienojakoisesti.

Mitä isompi termin arvo alun perin on, sen pahempaa jälkeä huononeminen ilmeisesti tekee. Jos huonon pyörän on pilattava kaikki termit, joissa se on mukana, on tietenkin järkevää toivoa että se on mukana etupäässä jo valmiiksi huonoissa termeissä. Eli niissä jotka ovat edellä kuvaillun tilastollisen hajonnan alapäässä. Voidaanko jollain yleisellä perusteella sanoa, että jokin termi on huonompi kuin toinen? Väitän että voidaan. Tässä tapauksessa on vain astelukujen 0-2 termejä, eli enimmillään kerrotaan kaksi hyötysuhdetta keskenään (kuten P1P2). Otetaan toiseksi esimerkiksi 11:1-talja analyyseineen:

11:1

1 +
P1 + P2 +
P1P2 + P1P3 + P1P4 + P2P4 +
P1P2P3 + P1P2P4 + P1P3P4 +
P1P2P3P4

Esiintymistiheydet (suluissa 1., 2, 3, ja 4. asteen termien määrät):

• P1: 8 kertaa (1, 3, 3, 1)
• P2: 6 kertaa (1, 2, 2, 1)
• P3: 4 kertaa (0, 1, 2, 1)
• P4: 5 kertaa (0, 2, 2, 1)

P1 on mukana kolmessa ja loput kahdessa kolmannen asteen termissä. Kolmannen asteen termit ovat kertaluokkaa pienempiä jo siksi, että niitä on kerrottu kertaalleen enemmän jollain tosielämän hyötysuhteella (esimerkiksi 0,8*0,8*0,8 = 0,5). Mitä korkeampi aste, sen useamman pyörän läpi kulkevaa voiman reittiä termi edustaa. Neljännen asteen termi vastaa yksinkertaista 5:1-taljaa, jonka vahvuuksiin hyötysuhde ei tunnetusti kuulu. Toiseksi, mikäli N:n pyörän systeemissä on N:n asteen termi (aina ei ole), siinä joka tapauksessa on mukana kaikkien pyörien hyötysuhteet, eikä se siis tee mitään eroa pyörien välillä.

Termi P1P2P3P4

Joudun tällä erää jättämään asian hieman ilmaan. Aihe on siitä kiitollinen, että sitä pystyy tutkimaan simuloidun empirian keinoin, nimittäin laskemalla tietokoneella ison määrän erilaisia tapauksia ja mittaamalla niitä tilastollisesti. Kun nimittäin ei näköjään riitä älli analyyttiseen ratkaisuun, oikeaan matematiikkaan. Palannen asiaan!

Taaspa taljojen hyötysuhteista

En edes yritä saada tiivistettyä otsikkoon tämän pienen kenttätestin aihetta. Se olisi jotain sellaista kuin "mahdollisimman tehokkaat, pidätinlaitteettomat taljasysteemit" tai "kuinka saan reppuun mahtuvilla tarvikkeilla kahden muutaman metrin päässä toisistaan olevan ankkuripisteen väliin mahdollisimman helposti mahdollisimman suuren staattisen voiman". Vastaukseksi ei kelpaa "osta Motonetista vaijeritalja, 19,90€". Onneksi ei tarvitse perustella tätä kenellekään, koska en ehkä osaa. Tietenkin haluan selvitä kiipeilykamoilla, jotka muka ovat mukana muutenkin - tosin en tiedä missä mukana, jos nyt tässäkin käyttämääni arsenaalia katson. Ehkäpä perustelen asian itselleni niin, että tämä on maailmani, näillä mennään, ja näitä opiskellaan niin paljon kuin suinkin.

Testiasetelmaa

Voimat mitattiin Rock Exotica enForcerilla käyttäen maksimiarvon muistia, ja taljan sisään vedetyn voiman normalisoin mainiolla Clas Ohlsonin matkalaukkuvaa'alla. Ei, se ei oikeasti ole mainio, koska se yrittää löytää arvon johon voima asettuu, joten jossain vaiheessa vetoa se todellakin sitten asettuu. Silti uskon, että tällä vaa'alla mitattu 30 kg vastaa riittävän tarkasti 0,3 kN voimaa.

Tutkailin tässä lyhyessä sessiossa eräänlaista nelikenttää. Ensinnäkin A) z-rig, jota vedetään toisella z-rigillä, jolloin lopputuloksena on teoreettisesti 9:1. Sitten B) tästä kehitelty kompleksi versio. B:n laskennallinen taljasuhde on 11:1.

A) "Z rig on Z rig", 9:1

B) 11:1

Nelikentän toisen reunan muodostavat systeemit, joissa toisen z-rigin korvaa simppeli 5:1. C) talja, jota käytän mielestäni perustellusti slacklinen kiristämiseen: 5:1 jota vedetään z-rigillä. Palaan perusteluihin.

C) "Z rig on 5:1", 15:1

Neljäs ruutu on D) vastaavalla tempulla parannettu C, kuin mitä A:lle tehtiin että saatiin B. Laskennallinen taljasuhde on 19:1. Ehkä jo tässä vaiheessa voisi huomauttaa, että 19:1 on aikuiselle ihmiselle tolkuton suhde. Jos pystyy vetämään vaikkapa 0,6 kN köyteen, huonollakin hyötysuhteella tällainen talja tuottaa helposti sellaisia voimia, että pitää todella laskea solmujen, tarrainten ja köysipyörien kokemat voimat.

D) Sama C:lle kuin B oli A:lle, 19:1

Mitäs tässä lässyttämään, tulokset tiskiin. Kutakin taljaa vedettiin siis rauhallisella, 0,3 kN kohdalla loppuvalla vedolla. En toistellut. Teen ehkä joku päivä hieman tieteellisemmällä otteella paremman tutkimuksen.

• A) 1,9 kN
• B) 2,3 kN
• C) 2,9 kN
• D) 3,8 kN

Jos sitten verrataan näitä lukuja laskennallisiin (esimerkiksi A:n pitäisi 0,3 kN voimalla tuottaa 9 x 0,3kN = 2,7kN), saadaan hyötysuhde (todellinen/laskennallinen) ja todellinen taljasuhde:

• A) 70%, 6,3:1
• B) 70%, 7,8:1
• C) 65%, 9,8:1
• D) 66%, 12,6:1

Kiinnostavan tylsää. Jos systeemissä on simppeli 5:1, hyötysuhde on 65%. Jos taas pidättäytyy korkeintaan z-rigeissä, hyötysuhde on 70%. Melkein kuin oppikirjasta, vaikkakin melkein sanoisin hyötysuhteita suhteellisen hyviksi. Aiemmin mittasin kahden kuulalaakeroidun pyörän varaan rakennetun z-rigin hyötysuhteeksi 82%. Jos tällaisia laittaa peräkkäin kaksi kappaletta, teoriassa toisesta päästä tulee ulos sisään laitetusta energiasta 82% x 82 % = 67%. Ai kun nättiä! Oikeasti nyt mitatulla datalla ei kylläkään pitäisi puhua yhden prosenttiyksikön tarkkuudella.

Ehkä vielä muutama sana systeemeistä.

A:n kauneus on yksinkertaisuudessa. Se on yksinkertaisin rakentaa, helppo tunnistaa, ja siinä on vain yksi tarrain. Toki pitää muistaa, että kaikissa systeemeissä vasemmanpuolinen punainen ankkurilevy korvaa yhden tarraimen, jos vertaa tilanteeseen jossa systeemillä olisi tarkoitus nostaa jotain pidempi matka, jolloin systeemiä pitäisi pystyä resetoimaan välillä. Silloin pitäisi tietenkin lisäksi korvata oranssi pyörä jonkinlaisella pidättävällä laitteella (tai lisätä pyörään prusik). Yhteensä kolme tarrainta B:n tapauksessa moninkertaistaa riskin, että jokin tarrain törmää ennen pitkää köysipyörään. Ja joka tapauksessa huolehdittavaa on enemmän. Lisäksi systeemi vaatii taatusti paljon enemmän tilaa kuin A.

A:ssa on myös se tyylikäs piirre B:hen verrattuna, että kuorma jakautuu tolkullisessa suhteessa (3:1) oranssille ja metallinväriselle pyörälle, kun B:ssä yksi pyörä kantaa 8/9.

Pidän systeemin C yksinkertaisuudesta ja säädettävyydestä sekä siitä, että kun laitan oranssin yksinkertaisen taljapyörän tilalle I'D:n, saan juuri sopivassa kohdassa olevan PCD:n jonka kuorma säilyy juuri sopivan kohtuullisena slackline-käytössä. Siinä tapauksessa ei tietenkään pidä edes optmimismin puuskassa puhua 15:1:stä.

D todellakin on aika yliampuva, koska reippasotteinen käyttäjä saattaa sillä yksin ylikuormittaa heppoisen taljapyörän. Joskus silti saattaa olla hyödyllistä pystyä tuottamaan isohko voima leppoisalla vedolla. Olen esimerkiksi kokeillut joitain yksittäisiä ankkuripisteitä  6kN voimalla. Jos haluaa saada tällaisen voiman aikaan tasaisella, rauhallisella vedolla ja yksin, ei 11:1 riitä. Ja miksi rehkiä, jos kerrankin selviää käyttämällä päätään.

Mielipide mikrohalkeamista

Haa, onnistuin muodostamaan mielipiteen pudotettujen kiipeilykamojen käyttökelpoisuuden ikuisesta kysymyksestä! En väitä että tämä olisi totuus, muodosta ihmeessä oma käsityksesi. En myöskään lupaa ettei mieleni vielä muuttuisi.

Ei ole tieteellistä näyttöä, että korkealtakaan kovalle alustalle pudonnut, päällisin puolin ehjä laite olisi heikompi kuin pudottamaton vastaava laite. Ja näyttöä on haettu useaan kertaan; otannat ovat olleet riittävän suuria, pudotuskorkeutta riittävästi (esim. 30 m) ja alustana betonilaatta. On sekä tehty vetolujuuskokeet että etsitty murtumia rötgenkuvilla. Jopa El Capitanin satoja metrejä korkean Salathe wallin alta löytyneistä sulkurenkaista on etsitty selvästi heikentyneitä - turhaan.

http://www.outdoorsafetyinstitute.com/index.php/news/single/should_you_retire_a_dropped_carabiner/
https://fatcanyoners.org/bush-guide/dropped-carabiners/

Ei myöskään tunneta tapauksia, joissa aiemmin pudonnut sulkurengas olisi pettänyt käytössä - itse asiassa käytössä katkeilevat sulkurenkaat taitavat loistaa poissaolollaan ylipäätään.

Oletettujen mikrohalkeamien vaarana pidetään ilmeisesti vaihtokuorman (eli toistuvan kuormittamisen) murtumaa kasvattavaa vaikutusta. Alkusärö vaikuttaa oleellisesti kappaleen väsymiseen eli rikkoutumiseen vaihtokuorman alla. Kiipeilylaitteiden kuormitustestit eivät sisällä vaihtokuormituskoetta, koska alkusärö vaikuttaa myös vetomurtolujuuteen. Kun suunnittelukerroin murtolujuuden suhteen on riittävän suuri, eli käyttökuorma on riittävän pieni suhteessa murtolujuuteen, ei käyttökuorman luokkaa olevalla vaihtokuormallakaan tule kestävyysongelmia. Tai näin oletan päättelyketjun kulkevan.

Vaikuttaa siltä, että mikrohalkeamat ovat myytti. Eräät selittävät alkuperäksi 50-luvun valurautaiset nousukahvat, jotka todellakin saattavat murtua ns. hauraalla mekanismilla ja siis saada merkittäviä, huomaamattomia murtumia pudotessaan. Itse asiassa monet kiipeilytekniikkaa tuntevat lähtevät siitä, että  mikrohalkeamat eivät ole todellisia, mutta vetoavat kuitenkin siihen, että kun nyt kerran on herännyt epäilys laitteen (tyypillisesti sulkurengas tai varmistuslaite) turvallisuudesta, on parempi heittää se menemään ja ostaa uusi. Epäilys toki kaivertaa mieltä ja vaikuttaa kiipeilyyn koko ajan.

Tämä "ne ovat halpoja" -argumentti kuitenkin selvästi ontuu. Ensinnäkin argumentti pätee yhtä hyvin vaikka mustaan magiaan: jos alkaa pelätä että noita on kironnut laskeutumislaitteen, tietenkin on ikävä laskea henkensä sen varaan. Argumentin perusteella siis pitäisi uusia laite koska "se on halpa", eikä esimerkiksi selvittää, onko mustalle magialle mitään näyttöä. Toiseksi, köyden päälle astuminen on samantyyppinen asia kuin laitteiden (matalaltakaan) pudottaminen; kaikki tietävät ettei sitä saisi tehdä, ja kiellolle on myös järkevä perustelu. Tieteellistä näyttöä köyden heikkenemisestä hiekanjyvien tunkeutuessa ytimeen on luultavasti yhtä paljon kuin mikrohalkeamien vaikutuksesta sulkurenkaan lujuuteen. Silti kukaan ei uusi köyttä pelkän päälle tallomisen takia, koska se ei ole halpa. Tuskin kukaan kuitenkaan suoraan sanoo, että köysi on juuri sen verran kallis että riski kannattaa.

On silti mahdollista, että metallista/muovista valmistettu kiipeilylaite rikkoutuu vaarallisesti pudotessaan, selvähän se. Tietenkin pudonneet laitteet on erityisesti tarkastettava (kuten kaikki laitteet säännöllisin välein). Oleellinen kysymys kuuluu, kuka osaa tehdä tällaisen aistinvaraisen tarkastuksen riittävän hyvin.

Putoaminen on myös erityisesti kiipeilylaitteita koskeva riski. On toki muitakin mekanismeja, joilla ne saattavat vaurioitua, mutta olisi saivartelua verrata niitä putoamiseen. Veneen avaimiin saa kelluvia avaimenperiä, koska niiden suurin uhka ei ole vaikkapa jäädä puristuksiin painavien asioiden alle. Kun siis kiinnitetään erityistä huomiota putoamisiin, saadaan haaviin valtaosa kiipeilyyn liittyvistä tilanteista joissa huomaamattomia vaurioita saattaa syntyä.

Sanan "mikro" yksi tavallinen määritelmä on "niin pieni, ettei sitä näe paljain silmin". Tavallaan voisi sanoa, että jos laite on (pudotessa) rikkoutunut vaarallisesti, mutta tarkastaja ei huomaa vaikkapa kokonaan puuttuvaa osaa, kyseessä on "mikrohalkeama". On myös huomattavasti mukavampi kuulla perusteluksi sille, ettei ole pätevä tekemään aistinvaraista tarkastusta se, että "mikrohalkeama" saattaa jäädä näkemättä kuin se, että ehkä on sokea jollekin isolle vialle. Ihminenhän todella saattaa olla hyvinkin sokea asioille, joita ei sillä hetkellä ymmärrä tai vain satu näkemään. Me kaikki, kokeneet ja kiipeilylaitteista erityisen kiinnostuneet mukaan lukien.

Voi ajatella, että mikrohalkeamiin vetoaminen on kohtelias ja pedagogisesti tiedostava tapa sanoa, että jokin sinänsä aistinvaraisesti havaittavissa oleva vika saattaa jäädä huomaamatta. Terveellä tavalla skeptinen ihminen osaa olla skeptinen myös omia aistejaan kohtaan, ymmärtää erehtyväisyytensä ja hyväksyy sen ettei välttämättä kykene tarkastamaan mahdollisesti rikkoutunutta laitetta riittävän hyvin. Jokainen ohjaajan, kouluttajan tai muuhun asiantuntemusta edellyttävään rooliin joutunut saa itse miettiä, onko liian holhoavaa ja elitististä olla kertomatta tätä totuutta (?) myös vielä kokemattomammille ja ehkä teknisesti vähemmän orientoituneille kiipeilijöille.

Jokin määrä mikrohalkeamamyyttiä lienee terveellistä kiipeily-yhteisölle. Jos tämä uskomus säästää vuosien mittaan joitakin ihmishenkiä maailmalla, niin kenties se on painavampi asia kuin hyvien laitteiden turhan romuttamisen epäekologinen kulttuuri (käytännössä tosin valtaosa taitaa siirtyä uudelle omistajalle, joka mielellään "romuttaa laitteen" vuosien käytön myötä). Itse saan ison immuunireaktion kaikista sellaisista uskomuksista tai tavoista, jotka eivät perustu totuuteen vaan tavalla tai toisella erehdyttävät ihmiset toimimaan oikealla tavalla.

Ankkurin piteneminen ja iskukuorma

Aiemmin löydettiin ihan konkreettisesti ankkurin pitenemisen aiheuttamat kaksi piikkiä, ja aihetta on tullut spekuloitua jonkin verran. Nyt ryhdistäydyin ja edes yritin liittää aiheeseen jotain empiriaa.

Yritän olla ytimekäs: Kun ankkuri pitenee yhden pisteen pettäessä ja kuorman romahtaessa muiden pisteiden varaan, näiden pisteiden kokema iskukuorma koostuu ainakin kahdesta osasta. Primäärinen (ajallisesti) johtuu siitä, että kuorman ja ankkurin yhdistävä materiaali, lähinnä köysi, toimii jousen tavoin ja räpsähtää lyhemmäksi, niin että ankkurin massiivisten osien (kuten sulkurenkaat) ja osin itse köyden massa paiskautuu ankkurimateriaalia vasten. Jos ja kun ankkurimateriaali yleensää on mahdollisimman vähäjoustoista, saattavat pisteet kokea hyvin terävän iskukuorman. Tuossa viitatussa aiemmassa kokeessa tämä isku oli noin 0,1 s pisteen pettämisen jälkeen, ja voimahuippu n. 3,3 kN.

Sekundäärinen isku, edelleen lähinnä ajallisesti, on sitten se helpommin ymmärrettävä: kuorman putoaminen uuteen asemaansa. Kokeessamme tämä tapahtui kohdalla 1 s ja huoppukuorma oli 2,6 kN. Nämä arvot eivät tietenkään ole mitään yleispäteviä, vaan riippuvat tapauksesta. Oletan, että testin tapaus (köysirata, melko paljon köyttä) korostavat primääristä iskua.

Perustelen oletukseni. Ensimmäinen isku vaatii köyteen sen verran venymää, että vapautettuna tämän venymän jousiefekti viskaa ankkurin massiivisia osia päin ankkurin löystyneitä osia. Puhutaan yksinkertaisuuden vuoksi sulkurenkaasta (master point) ja slingistä, kuten sliding x -ankkurissa on. Siis köyden "jousimaisuuden" on riitettävä paiskaamaan master point riittävän lujaa päin slingin loppupäätä. Kiristetyn köyden jännitys tietenkin vastaa kiristävää kuormaa, vaikkapa suoraan köydessä roikkuvaa massaa. Mutta se, kuinka jännitys pienenee kun köyden annetaan lyhetä esimerkiksi kymmenen senttiä, riippuu köyden dynaamisuudesta ja tietenkin pituudesta. Lyhyt pätkä vaijeria tai superstaattista polyesterinauhaa venyy sadan kilon kuormalla joitain millimetrejä, joten on helppoa ymmärtää ettei sellainen toimi "ritsana" yhtä hyvin kuin 30 metriä staattista köyttä (kuten testin köysiradassa), dynaamisesta puhumattakaan - vaikka kuormana olisi täsmälleen sama sata kiloa.

Toiseksi köysiradan tapauksessa ankkurin piteneminen kasvattaa "sagia", eli helpottaa ankkurikulmia. Ankkurikulma ei vaikuta pätkääkään primääriseen iskukuormaan, mutta sekundääriseen kylläkin. Testissämme helpompaan kulmaan pudonneen köysiradan lopullinen kuorma oli tasan puolet alkuperäisestä, eli jäljelle jäänyt piste kantoi saman kuorman kuin alkutilassa, jossa se jakoi kuorman toisen pisteen kanssa.

Sain köysiratatestistä kommentin, jota en aluksi ymmärtänyt. Eräs ehdotti, että koe pitäisi toistaa myös yläköydessä riippuvalla massalla. En heti tajunnut, että nämä kaksi piikkiä voidaan saada myös siinä tapauksessa. Jos joku olisi näyttänyt silloin tämän kuvan, olisin tajunnut heti:

Pettävä ankkuri, masterpointin massa, köysi eli jousi, kuorman massa

Painovoima on siitä hauska juttu, että se vaikuttaa kappaleisiin samassa suhteessa kuin kappaleen massahitaus jarruttaa kappaleen kiihdyttämistä. Siispä kaikki kappaleet putoavat samalla kiihtyvyydellä. Toki koko kuvan hässäkkä lähtee putoamaan alaspäin, mutta ankkurin ja kuormana toimivan massan yhdistävä köysi pyrkii samalla lyhenemään, vetäen ankkuria ja massaa toisiaan kohti. Kun ankkuri nyt kuitenkin käytännössä on kevyempi kuin kuorma, alle sadasosan kuorman massasta, voi yksinkertaisesti olettaa että jousi vain vetää ankkuria kohti kuormaa. Joka tapauksessa ankkurin vauhti kiihtyy aina kovemmin kuin kuorman.

Jos jousi on riittävän pitkä eikä liian jäykkä (eli köysi liian staattinen), kuorma on ehkä venyttänyt sitä selvästi enemmän kuin mitä ankkuri pitenee. 50-metristä staattistakin köyttä saa taljata pari metriä ennen kuin siinä on sadan kilon kuorma. Hyvässä tapauksessa tuo puolen metrin luokkaa oleva ankkurin piteneminen päästää köyden jännityksestä vaikkapa vain 30%, niin että jos alussa köysijousi kiskoo ankkuria kohti kuormaa sataa kiloa vastaavalla voimalla, niin vielä puolen metrin päässäkin 70 kiloa vastaava voima kiskoo sulkurenkaaseen lisää vauhtia - kunnes sulkurengas paukahtaa slingin päätyyn.

Eikä tässä vielä kaikki! Mikäli köydessä todella on jäljellä tuo 70 kiloa vastaava voima siinä vaiheessa, kun ankkurin piteneminen loppuu väkivaltaisesti, ei kuorma todellakaan putoa löysän köyden varaan. Vai mikä putoamiskerroin se on, jos köysi jo valmiiksi kannattelee satakiloista kappaletta 70 kg vastaavalla voimalla? Kun painovoima lisätään, nettovaikutukseksi jää 30-kiloisen kappaleen painovoima kiihdyttämään 100-kiloista massaa. Tulee mieleen vanhat filmit kuusta.

Melkein käytäntöä, nimittäin internet-empiriaa: Beal ei kerro lempiköyteni Access 11 mm Unicoren venyvyyttä, mutta esimerkiksi Sterling Superstatic 11 mm venyy 300 paunan (136 kg) kuormalla 3,9%. Jos nyt oletetaan, että köysi on lineaarinen jousi, eli että se venyy kaksinkertaisen määrän mikäli voiman kaksinkertaistaa, saadaan venymäksi 100 kg kuormalla 2,9%. Siispä viidenkymmenen metrin matkalle sadan kilon kuormalla tulee venymää 140 cm - kutakuinkin kaksi kertaa se, mitä 150 cm slingistä tehndyn sliding x:n piteneminen olisi pisteen pettäessä. Eli lineaarisen jousen oletuksella 50 metrin staattisellakin köydellä 70 cm lyheneminen vain puolittaisi köydessä olevan jännityksen.

Suomeksi sanottuna, riittävän pitkällä köydellä voisi käydä näin: Ankkurin toinen piste pettää, köysi räpsähtää uuteen, edelleen kireään asentoon. Tähän kuluu luokkaa 0,1 s, eikä köydessä roikkuva kuorma juurikaan ehdi reagoida. Koska köysi ei ole aivan niin kireä kuin alun perin, painovoima onnistuu kuitenkin kiskomaan kuormaa alaspäin, ja alimman pisteensä kuorma saavuttaa vaikkapa sekunnin kuluttua. Ainoa hetki, jolloin mikään materiaali oli kokonaan kuormaton, oli ensimmäisen 0,1 sekunnin aikana, kun ankkuri oli lyhenemässä, joten vain primäärinen iskukuorma on todella isku.

Toinen ääripää olisi sitten täysin joustamaton tai hyvin lyhyt köysi tai muu ankkurin ja kuorman yhdistävä asia. Ainakin voi sanoa, että jos yhdistävä materiaali on kuormitettuna lyhempi kuin ankkurin piteneminen, ei mikään määrä joustoa saa aikaan primääristä iskua. Kuorma ja masterpoint putoavat yhtenä möykkynä painovoiman vetämänä niin alas kuin pidentynyt ankkuri päästää, ja sitten massa rämähtää jäljelle jääneen pisteen varaan. Nyt kaikki osat ovat vapaassa pudotuksessa, kunnes kaikki liike-energia menee sekundääriseen iskukuormaan.

Pettävä ankkuri, masterpointin massa, hyvin staattinen ja lyhyt köysi, kuorman massa

Sitten oikeaa käytäntöä

Ajateltiin Jukan kanssa vähän leikkiä, vaikka tiedettiin ettei mitään näin pitkiä köysiä saadakaan roikkumaan, tai aikanaan kunnollista testikuormaa niiden varaan. Viritettiin suhteellisen jäykkään ankkuriin, muuan sillan tukirakenteisiin, sliding x -ankkuri ja ripustettiin siihen Aleksis III, 100-kiloiseksi punnituksessa todettu kivenmurikka. Ankkurin ja Aleksiksen väliin ei valitettavasti saatu kuin surkeat viisi metriä köyttä, vaikka olin toivonut edes kahdeksaa.

Jotain oli jo opittu, mutta paljon oli opittavaa jäljellä. Olin ajatellut, että ankkuripisteen pettämisen simuloiminen olisi näppärintä katkaisemalla shuntin läpi (ulos ja saman tien takaisin sisään) kulkevan köysilenkin kanssa. Näin ei tarvitsisi solmia mitään, ja köyttäkin kuluisi minimimäärä per pudotus. Kuvasta voi tihrustaa.

Oikealla jäljelle jäävä piste ja voimamittari, vasemmalla pettävä piste (huono versio)

Tiesin ennestään, että shunt luistaa herkästi jos siinä on kaksi köyttä, tai jopa sama köysi kahteen kertaan. Mutta jotenkin ajattelin, ettei se haittaisi. Tiesin myös ennestään, että sliding x ei tosiaankaan tasapainota itseään kovin täydellisesti, vaan se tarvitsee apua, jopa isommalla kulmalla kuin kuvassa olevalla turhan pienellä. Mutta jotenkin yllätyin, kun vasen, pettäväksi suunniteltu pää oli niin löysä kuin se sliding x:n luistamatta voi olla - eli hyvin löysä. Masterpointin kitka kantaa yllättävän ison kuorman. Kaikki tämä on ilmiselvää näin jälkeenpäin; tietysti systeemi on kuin suunniteltu etsimään kehnoin mahdollinen tasapainotus. Ja vielä huonoon suuntaan. Nimittäin kun tuo sininen köysi katkaistiin, sliding x valui kaikessa rauhassa pitkäksi. Mittausdataa ei saatu, koska enForcerin pienin liipaisukuorma on 2 kN, ja ei, sitä lähellekään ei päästy. Jatkossa sitten käynnistinkin mittaukset käsin.

No eipä siinä, tämä oli helppoa korjata. Samalla keksittiin vahingossa jo toisen kerran, kuinka tällaisissa mittauksissa kannattaa nostaa pudotettava kuorma takaisin ylös. Ei kannata haulata ulkoisella systeemillä testiköydestä, vaan kiskoa suoraan sitä maillonia, joka katkaistavaan köyteen tulee - eli väkisin vetää itse sliding x takaisin muotoonsa, kyllä se kuorma sieltä seuraa. Edelleen tajuttiin, ettei maillonia edes kannata ripustaa mihinkään muuhun pisteeseen, vaan antaa roikkua taljassa katkaisemiseen asti. Hieno juttu, mutta tämän niksin olisi pitänyt olla jo työkalupakissa viime kerran jäljiltä, jolloin Jukka sen hoksasi.

Valumaton pettävä piste suoraan taljassa ja parempi ankkurikulma. Ja nätisti 50 kg puntarissa!

120 cm slingi sliding x:nä, 100 kg kuorma, 5 m köyttä, kevyemmät metallikamat ankkurissa

Kuten arvata saattoi, viisi surkeaa metriä dynaamistakaan köyttä ei juuri saanut aikaan primääristä iskua. Pisteen kuorma putoaa nollaan, eikä käyrästä oikein voi päätellä, missä vaiheessa slingi oli suorana. Sen voi kuitenkin päätellä, ettei mitään radikaalia master pointin ja slingin päädyn törmäystä tullut.

Seuraavaksi vaihdettiin slingi 150-senttiseksi ja ehkä liukkaammaksikin. Alla olevassa kuvassa on myös jo vaihdettu masterpointiin teräksinen ovaalisulkurengas 8 mm delta-maillonin tilalle ja 10 mm ovaalimaillon lähellä katkaisupistettä olleen 8 mm ovaalimaillonin tilalle. Tarkoituksena oli siis kokeilla liikkuvien osien massan vaikutusta. Alla on molempien testien kuvaajat.

150-senttinen slingi ja Jukka valmiina katkaisemaan

150 cm slingi sliding x:nä, 100 kg kuorma, 5 m köyttä, kevyemmät metallikamat ankkurissa

150 cm slingi sliding x:nä, 100 kg kuorma, 5 m köyttä, raskaammat metallikamat ankkurissa

Mitään kovin uskottavaa eroa ei kevyiden ja raskaampien ankkuritarpeiden välille oikein pysty perustelemaan. Mutta ei sinänsä pitäisi pystyäkään, koska koko primäärinen iskukuorma puuttuu. Alla olevaa kuvaa tutkimalla voi yrittää hahmottaa, miltä ankkurin lyheneminen näyttää käytännössä (olispa suurnopeuskamera...). Maillon, joka yhdisti slingin pettäneeseen pisteeseen, liikkuu tietenkin kaksinkertaisella nopeudella verrattuna master pointiin (ovaalisulkurengas). Koska kappaleen liike-energia on lineaarisesti verrannollinen kappaleen massaan mutta nopeuden neliöön, riittää että edellisen maillonin massa on neljäsosa sulkurenkaan massasta, että niiden liike-energiat olisivat yhtä suuret. Liike-energia siis pesiytyy mieluummin nopeasti liikkuviin kuin massiivisiin kappaleisiin. Tätä täytyy tutkia joskus mittaamalla!

Pitenemisen lopputulos raskaammilla metallikamoilla (anteeksi surkea kuva)

Esimerkki kuormitetun sliding x:n huonosta tasapainottavuudesta. Yritän liu'uttaa kuormaa enemmän mittarin varaan, ja siis sitä todella pitää suostutella, vaikka mittari näyttää reilun viidenkymmenen sijasta 28 kg. Tämän "tasapainottavan" ankkurin toisen pisteen varassa on siis oltava vähintään 72 kg.

Seuraavaksi puolitettiin köyden määrä, kun ei kerran pidentääkään voitu! 75 cm pitenemisellä ja 2,5 metrillä dynaamista köyttä saatiin sentään neljä kilonewtonia rikki. Ei sen enempää eikä vähempää primääristä iskua - vaiheet ennen sekundääristä iskua ovat hyvin samannäköiset kuin pidemmällä köydellä.

150 cm slingi sliding x:nä, 100 kg kuorma, 2,5 m köyttä, raskaammat metallikamat ankkurissa

Entäs jos?

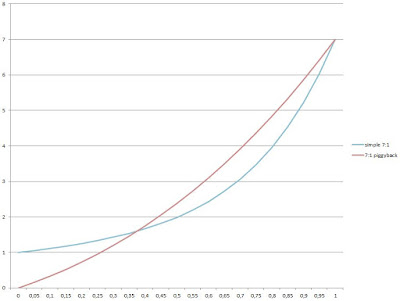
Mutta mitä jos primääristä iskua tutkisi erikseen? Viimeisestä testistä nähtiin, että 150-senttisellä slingillä ja lyhyellä köydellä sekundäärinen isku alkaa 0,4 sekuntia pisteen pettämisen jälkeen ja on huipussaan 0,6 sekuntia pettämisen jälkeen. Jos olettaisi, että ainakin tämän sekunnin puolikkaan alkuvaiheissa kuormaa voi tosiaan pitää kiinteänä ankkurina, ikään kuin ilmaan pultattuna pisteenä? Ja sitten, jos koko systeemin kääntäisi vaakatasoon, koska tavallisella tallaajalla on hyvin vähän mahdollisuuksia ripustaa satakiloisia esineitä kymmeniä metrejä pitkän köyden varaan (huokaus).

Alla olevassa kuvaajassa on esitetty kappaleen putoaminen maan vetovoimakentässä (putoamiskiihtyvyys 9,81 m/s2) ilman ilmanvastuksen vaikutusta. Ilmanvastushan hidastaa putoamista, joten missään tapauksessa vapaassa pudotuksessa oleva kappale ei tämän nopeammin kiihdy. Siispä esimerkiksi 0,5 m rajapyykki ei kerta kaikkiaan tule ylitetyksi ennen 0,3 sekuntia pudotuksesta. Tietenkin jokainen sentti, jonka kuorma vajoaa alaspäin, kiristää osaltaan köyttä eli lisää voimaa, jolla masterpointia kiskotaan alaspäin kohti törmäystä. Mutta voisihan ainakin tutkia, millä aikaskaalalla primäärinen törmäys ylipäätään tapahtuu (ilmaan mainittua kiristymistä) ja sitten tutkia käyrältä, millainen vajoaminen maksimissaan olisi odotettavissa, mikäli köyden päässä olisi todellinen taakka. Ja edelleen mitata, millainen ero köyden jännityksessä on, mikäli sitä kiristää sen matkan, joka vajoamisen takia jäi puuttumaan. Kenties voitaisiin osoittaa, että kiinteiden pisteiden avulla mittaaminen toimii riittävän hyvin.

No totta kai tämä piti kokeilla. Järjestelin pihalle seuraavanlaisen systeemin: kahden puun välissä oli 20 metriä dynaamista sinkkuköyttä. Toisessa päässä ("kuorman pää") köysi oli Rigissä, toisessa ("ankkuripää") se oli kahdeksikolla sliding x -ankkurissa, joka oli toisesta päästään voimamittarin kautta mahdollisimman jäykästi kiinnitetty. Toinen pää oli köydessä, jonka raaskii katkaista.

Ankkuripää

Kuorman pää

Sekä tässä uhrattavassa köydessä (sininen), että kuorman päässä testiköydessä oli z-rig. PCD:nä jo mainittu Rig ja sinisessä köydessä I'D. Tarkoitus oli kiskoa punaiseen testiköyteen 1 kN eli sadan kilogramman taakkaa vastaava voima ja samalla tutkia, kuinka paljon köyttä on kiskottava sisään tällä voimalla. Siksi merkitsin lähellä kuorman päätä, 20 cm välein asteikon teipillä, alkaen sattumanvaraisesta kohdasta (0 cm ei siis tarkoita 0 kN). Kiristin aina uuden teipin kiintopisteenä toimineen jalustan kohdalle ja kuuntelin kauniin ja kätevän vaimoni toisesta päästä huikkaaman voimalukeman. Koska mittareita on vain yksi (joulupukilleko kirjettä?), jouduin olemaan luova. Oikeasti tässä vaiheessa sliding x ei ollut ihan valmis, vaan molemmat päät oli ripustettu voimamittariin:

Vippaskonsti voiman mittaamiseksi

Kuvan sininen köysi on tietysti se testattavan sliding x:n toinen piste, joka vain pitää vetää omalla taljallaan oikealle paikalle ja poistaa kuvan alempi sulkurengas siinä matkalla. Joku näppärä (esim. allekirjoittanut vielä vuosi sitten) olisi tietysti mitannut köyden voiman suoraan "tasapainotetun" ankkurin toisesta pisteestä, kahden kertotaulua apuna käyttäen, mutta johan se tässäkin tekstissä kerran todettiin, ettei siitä oikeasti tule mitään. Mieluummin luotan siihen, että kun näin pitkällä köydellä pisteen "nostaa" taljalla irti ja siirtää samalle tasalle kuvan tilanteen kanssa, saadaan riittävän tarkasti sama voima köyteen.

Dynaamisen köyden kiristäminen jopa tällaiselle mukavuusalueella olevalle jännitykselle on hieman turhauttavaa. Köysi asettuu ja voima hupenee, joten köyden jousivakio ei ole vakio vaan ajan funktio, eli voima riippuu venytyksen määrästä ja asettumisajasta. Pitämällä köyttä muutaman minuutin kilonewtonin voimalla jännitettynä ja tarvittaessa lisää kiristellen saatiin kuitenkin tuo kilonewton pysymään riittäävän kauan koetta varten. Jokaista toistoa varten toki kiristettiin uudestaan. Alla olevasta kuvaajasta näkee selvästi, miten köydestä lähti ensimmäisellä kiristämisellä "löysät pois", kun taas ensimmäinen löysääminen ja toinen kiristäminen kulkevat yllättävän samaa polkua. Jos niiden mukaan piirtää pienen suoran pätkän, saadaan 700 N/m, ja koska köyden pituus oli 20 metriä, yhtä metriä kohden jousivakiota tulee 14 kN/m. Ehkäpä sellaisessa nyrkkisäännössä voisi olla jotain järkeä, että jokainen kymmenen metrin pätkä tätä köyttä venyy 70 cm kilonewtonia kohden. Tai se, että köyden venyvyys 100 kg kuormalla on 7%.

Hystereesikuvaajaa köyden jännityksestä. Kolmiot ovat olevinaan nuolia, jotka osoittavat kiristämissen ja löysäämisen käyrät.

Siirtämässä pettävää ankkurin päätä köyden varaan

Ankkuri petti tänään yhteensä neljä kertaa, kaksi kertaa kahdella eri ankkurimateriaaleilla, vastaavasti kuin sillalla aiemmin. Kevyempi versio oli 8 mm delta-maillon masterpointissa ja 8 mm ovaalimaillon pettävässä päässä. Raskas oli taas teräsovaali (nyt Petzl Oxan) ja 10 mm ovaalimaillon. Kunkin ankkurimallin molemmat käyrät on laitettu alla samalle kuvaajalle. Järjestysnumero ilmoittaa mittausjärjestyksen, sijainti aika-akselilla on satunnainen (selvyyden vuoksi siirretty erilleen).

Voima kevyemmillä osilla

Voima raskaammilla osilla

Nytpä ei ole mitään käsytystä, miksi toisella mittauskerralla neljästä saatiin selvästi suurin voimapiikki. Keksin tähän mennessä kaksi ja puoli teoriaa. Ensinnäkin nämä piikit ovat enForcerin 500 Hz:n näytteenottotaajuudellekin hyvin lyhyitä. Esimerkiksi juuri tuon suurimman piikin arvot ovat ... 0.06, 0.06, 0.1, 1.4, 2.31, 1.34, 0.64, 0.2, 0.32 jne. Siis neljän tuhannesosasekunnin aikana voima on ollut ainakin yli 1,4 kN, mutta vaikka mittari sinänsä kykenisi mittaamaan kuinka tarkasti, meillä on tasan tuo yksi näyte keskeltä tätä ajanaksoa. Näytteenottotaajuus eli resoluutio ei todellisuudessa riitä näin suuritaajuuksisien voimien mittaamiseen. Muut kolme mittausta kylläkin ovat hyvin uskottavasti linjassa.

Teoria kaksi on se, että ankkurin tasapainotus vaikuttaa hyvin paljon, aivan kuten sillalla ihan ensimmäisessä pudotuksessa. Kun "löysät" oli otettu pois, eli kitka kannatteli jo valmiiksi mittarin puolte, slingi lähinnä valui pidentyneeseen asentoon. Jos taas löysät on otettu pois siihen suuntaan, että pettävä piste kannattelee suurempaa osaa kuormasta, saadaan toki suurempi kiihtyvyys ankkurimateriaalille. Muuten hyvä, mutta kuvaaja ei tue tätä. Ehkä tasapainotuksella on jokin muu vaikutusmekanismi.

Teorian puolikas päälle on sitten se, että kun en älynnyt solmia sinistä narua aina samanmittaisella hännällä ja ehkä katkaisinkin eri kohdasta, pitempi pätkä köyttä saattaisi hyvinkin lisätä massallaan iskua. Laimea selitys, puoli pistettä.

Olisiko pitänyt älytä vakioida mailloniin jäävä köydenpätkä? Olivia ei välitä, Olivia syö jäniksenpapanoita.

Voimat olivat melko pieniä, mutta suhteessa suurempia kuin keväisessä köysiratakokeessa. Silloin saatiin 2,3-kertainen piikki yhden pisteen alkuperäiseen kuormaan nähden, kun nyt piikki oli 3-kertainen. Piikit ovat kevyellä ankkurilla 0,07 s pettämisen jälkeen ja raskaalla 0,09 s. Kuten ylempänä olevaa käyrää tutkimalla selviää, ei edes vapaassa pudotuksessa oleva taakka ehtisi pudota tässä ajassa kuin reilusti vajaat viisi senttiä. Ja siis taakkahan ei olisi vapaassa pudotuksessa, koska mitattu köyden lopullinen jännitys 75 cm pidentymisen jälkeen on luokkaa 0,25 kN. Mitatusta jousivakiosta päätellen voima olisi viidenkin sentin putoamisen jälkeen vain 0,035 kN suurempi kuin nyt, kun "kuorman pään" puu jökötti kiltisti paikallaan.

Yhteenveto kai olisi paikallaan.

• Sliding x ei tasapainota kovin hyvin itsekseen.
• Ainakaan viidellä metrillä dynaamista köyttä ja sadan kilon roikkuvalla massalla ei saa aikaan primääristä iskukuormaa, kun sliding x:ssä ei ole pitenemisen estoa ja se on tehty 150 cm slingistä.
• Primääristä iskukuormaa voi tutkia pitämällä köyttä kiinteiden pisteiden välillä jännityksessä, koska taakan putoamisen (vaikutuksen köyden jännitykseen) aikaskaala on paljon suurempi kuin primäärisen iskukuorman
• mutta köyteen on vaikeaa saada kovin täsmällistä vakiojännitystä muuten kuin roikuttamalla siinä sopivaa massaa.
• Primäärisen iskukuorman taajuus on niin korkea, ettei 500 Hz näytteenottotaajuus riitä kunnolla sen tutkimiseen. On myös hyvä kysymys, kuinka vakavasti näin lyhyeen impulssiin pitäisi suhtautua, vaikka amplitudi olisikin melko korkea.
• Ehkä vielä se, että tällaiset testiasetelmat kannattaa aina resetoida taljaamalla ankkuripiste paikalleen, ja jopa pitää piste koko ajan taljassa kiinni!

Köysipyörien hyötusuhteiden mittaamisesta

En tosiaankaan ollut täysin tyytyväinen menetelmiin, joilla mittasin aiemmin erilaisten köysipyörien (useimmat pyörättömiä) hyötysuhteita. Staattisessa tapauksessa (kuinka suuri on liikkumattoman köyden jännitysero pyörän eri puolilla) on ehkä mahdollista saada aikaan riittävän tasainen voima vetämällä rauhallisesti käsin. Lisäksi on helppoa ripustaa hitaasti tunnettu massa köyden varaan ja mitata toiselle puolelle pyörää päätyvä voima. Mutta dynaamisen tilanteen, eli liikekitkan alueella toimivan pyörän kohdalla tilanne on hankalampi.

Köyden olisi siis oltava jännitetty tunnetulla vakiovoimalla, tai jos voima vaihtelee, täytyisi pystyä yhdistämään voiman vaihtelu toisen puolen voiman mittausdataan. Lisäksi köyden tulisi liikkua. Nopeudella ei pitäisi olla merkitystä, jos oletetaan että liikekitka on oleellisesti sama kaikilla järkevillä köyden nopeuksilla. Mutta jos turvaudutaan kaikkein helpoimpaan tapaan tuottaa vakiovoima - joka on kannatella massaa painovoimakentässä levossa - on nopeuden pysyttävä vakiona. Muuten massan inertia tuo oman mausteensa voimaan.

Virhelähteiden hyväksyminen ja etenkin niiden merkitysten tunteminen on tietysti kauniin käytännöllinen ratkaisu. Esimerkiksi jos menetelmällä saadaan selvät ja toistettavat erot laitteiden välille, ei tarvitse kuin sulkea pois kunkin laitteen itsensä aiheuttama osuus virheestä, niin saadaan ainakin suuntaa-antavaa vertailudataa. Jos taas on huolissaan inertian vaikutuksesta massan nostamiseen tarvittavaan voimaan, ja oman köyttä vetävän kätensä inhimilliseen virheeseen, voisi olla hyvä mitata millaisia erilaisia mittaussuorituksia tarvitaan, että saadaan millaisiakin virheitä dataan. On mahdollista, että kuulalaakeroiduilla, ehkä jopa liukulaakeroiduillakin köysipyörillä lepo- ja liikekitkan ero on niin pieni, että riittäisi tehdä staattinen koe.

Sitten vielä yksi mittaustekninen nyanssi. Voima-anturini Rock Exotica enForcerin tarkkuudeksi ilmoitetaan 2%, mutta toisaalla (en enää löytänyt lähdettä, mutta häiritsevästi muistuu mieleen että se olisi ollut Rock Exotian sivulla) 0,2 kN kautta mittausalueen (0-20 kN). Mikäli jälkimmäiseen uskoo, ei mittarilla tietenkään kannata mitata kovin pieniä voimia. Silloin vaikka aiemmin käyttämäni 60 kg olisi liian pieni kuorma, ja vielä älyttömämpää olisi mitata vetopään voimaa sellaisella mittarilla. Oli miten oli, totta kai mittarin voi olettaa olevan parhaimmillaan, kun liikutaan mittausalueen keskivaiheilla ennemmin kuin ääripäissä.

Miten vain, keksin pienen parannuksen sekä paikallaan olevan että liikkuvan köyden tapaukseen. Edellisestä ehdin jo ottaa pienen koe-eränkin, jälkimmäiseen palaan joskus.

Ensinnäkin nostin kuormaa siten, että vedin köyden kireäksi käsivoimien sijasta 3:1-taljalla. Viritin taljan niin, että veto on alaspäin, kytkin köyteen nousukahvan ja astuin rauhallisesti painoni jalkalenkille. Toistin kolme kertaa. Systeemi on esitetty kuvassa alla. Köysi oli Beal Access 10,5 mm unicore, pyörä ylhäällä oksassa Petzl Fixe, deviaatio ja z-rigin pyörä oli kuvassa näkyvä Petzl Tandem Speed, traktorissa Petzl Partner ja Shunt. Puiden väli oli noin 4 m.

Referenssivoiman mittaaminen

Tulokset ovat alla. Koska en tietenkään onnistunut ajoittamaan jokaista painallusta samaan kohtaan enForcerin näytesarjaa, oli normalisoitava data. Tein sen etsimällä kunkin mittauksen huippuarvon ensimmäisen esiintymiskohdan ja siirtämällä sarjoja niin että nämä kohdat asettuvat samalle hetkelle.

Referenssivoiman kolme mittausta kohdistettuna

 Ihan vain katsomalla näitä käyriä ja vastaavia köysipyöristä mitattuja, päätin että otan tunnusluvuksi sen voiman, joka saadaan ottamalla keskiarvo niistä voimista, joita saadaan sekunnin mittaisella välillä, joka alkaa puoli sekuntia huipun jälkeen, Eli referenssin tapauksessa noin välillä 1,7s ... 2,7s. Alla näkyy käyrät, ja kaikkien noiden pisteiden keskiarvona saatiin 1,151 kN.

Referenssimittausten arvot normalisointivälillä

Siinäpä jo vähän esimakua hyötysuhteista. Ainoastaan Fixe ei ole kuulalaakeroitu. Jos hyötysuhteeksi olettaisi 100%, voisi laskeskella elopainoni olevan luokkaa 40 kg. Mutta silä ei ole väliä, koska joka tapauksessa nyt tiedetään, millainen voima systeemillä saadaan köyteen tuon kauempana olevan puun kohdalla. Siispä sinne testattava pyörä! Voimamittarin taas toin toiseen päähän, lähelle taljaa. Mikä on siksi viisasta, että bluetooth-yhteys on melkoisen hatara - ja välttämätön, jos aikoo saada mittausdatan talteen.

Big Pulley testipenkissä

 Tältä näyttivät kuvan Camp Big Pulleyn kurvit:

Camp Big Pulleyn data

Käsittelin siis datan aivan samalla lailla kuin referenssinkin. Huiput kohdakkain ja keskiarvo aikaväliltä huippu + 0,5s ... huippu + 1,5s, Tulokset ovat tässä:

No justiin. Heti kärkeen muistuu mieleen Micro Traxionille luvattu 91%. Jännä että se on 91%, eikä esimerkiksi 90%... Tai 80%. Pahoittelut siitä että taulukko on melkein järjestyksessä mutta ei ihan, en jaksa korjata.

Oli odotettua, että Rock Exotican Omni-Block (2" single) pieksi muut. Olisin ollut pettynyt, jos ei olisi piessyt. Sen sijaan on jännä, että Petzlin Partner pesi Campin vähän isomman Tethys Pro:n. No, marginaalit ovat niin pieniä, ettei ehkä pitäisi luottaa järjestykseen liikaa. Se kuitenkin näkyy selvästi, miten pyörän halkaisijan putoaminen kahden tuuman luokasta sellaiseen näppärän kokoiseen pudottaa hyötysuhteen 90% sarjasta 80%:iin.

En tosiaan vielä huutelisi piireissä tietäväni mitään todellisista hyötysuhteista. Etupäässä koko juttu on labrailun harjoittelemista. Nytkin taisin saada pari oivallusta, kuten että tämä staattiseksi ajattelemani mittaustilanne on tuollakin köyden määrällä melkoisen dynaaminen. Köysi venyy ja valuu vähitellen pyörän läpi, jossain vaiheessa (jota valitettavasti ei tässä voida mitata) pyörä ehkä pysähtyy, mutta ainakin voima pienenee koko mittauksen ajan. Uskoisin, että tämä johtuu köyden venymisestä kuorman alla, ja koska köysipyörällä todellakin on suurempi lepo- kuin liikekitka, venyminen ei näy siten että saatu löysä valuisi systeemin läpi takaisin ja laskisi taljan päässä roikkuvaa minua alaspäin, vaan ennemmin välittyy suoraan köyden toisessa päässä olevalle voimamittarille. Käy järkeen.

Itse asiassa lopulta mittasin tilannetta, jossa taljalla jännitetään köysipyörän läpi kulkevalla ködellä jousta, jonka jousivakiota ei tunneta. Jousi tietenkin on koko talja- ja mittaussysteemin läpi kulkeva yli 10-metrinen pätkä köyttä. Oppia ikä kaikki ja ensi kerralla uudet virheet! Ei niin että nuo arvot välttämättä olisivat virheellisiä - päin vastoin, jotain hyötysuhteen aspektia ne väkisinkin mittaavat. Jos absoluuttisissa arvoissa voisikin periaatteessa olla huomautettavaa, se hoituisi lainaamalla toinen mittari ja mittaamalla samaan aikaan pyörän kahta puolta. Nythän yhden mittarin rajoituksella jouduttiin vain olettamaan että kaikissa mittauksissa saadaan sama referenssivoima.